Hidráulica de captaciones de agua subterránea Parte I

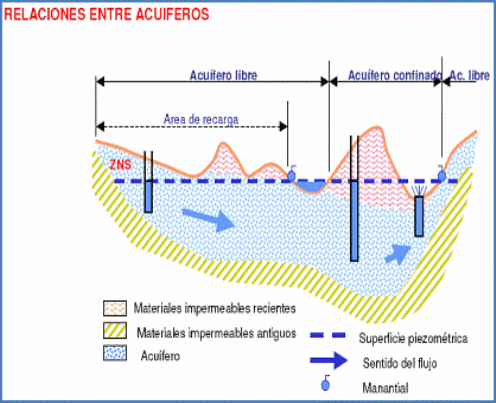
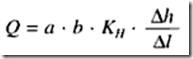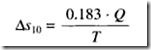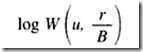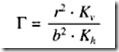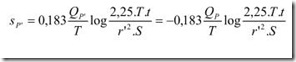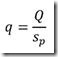El agua es uno de los recursos naturales más preciados del planeta. Más de mil millones de personas no disponen de agua potable, lo que provoca que cada año mueran unos tres millones y medio de personas, en su mayor parte niños, a causa de enfermedades relacionadas con la falta o el mal estado del agua. Por ello, la distribución equitativa y la explotación sostenible de este recurso se presentan como uno de los principales retos del siglo XXI. En la consecución de esta meta, los acuíferos pueden jugar un papel de vital relevancia.

La explotación racional de las aguas subterráneas constituye un elemento clave en el desarrollo económico de un país, área o región. En las regiones de clima semiárido o árido el agua subterránea tiene un interés estratégico. La explotación intensiva o incontrolada de las aguas subterráneas puede ocasionar, en determinados casos, ciertos problemas ambientales que favorezcan los procesos de desertización. En terrenos arenosos, el descenso del nivel freático puede favorecer la erosión eólica, la formación y el avance de las dunas. En regiones de gran aridez, el regadío con aguas de elevado contenido salino puede salinizar los suelos, obligando al abandono de tierras. Frecuentemente, la contribución de la explotación de las aguas subterráneas en los procesos de desertización queda enmascarada por la intervención de muchos otros factores.

Objetivos

Objetivos Generales:

· Proporcionar las herramientas teóricas y prácticas necesarias para comprender el funcionamiento hidráulico de los sistemas de aguas subterráneas para el diseño de obras de aprovechamiento y saneamiento.

Objetivos Específicos:

· Conocer la resolución de la ecuación general de flujo.

· Plantear y resolver problemas de hidráulica de pozos, en régimen permanente y variable. Interferencia entre pozos.

· Plantear y resolver problemas de Hidráulica de Captaciones Horinzontales y Sistemas de Drenaje en régimen permanente.

Conceptos fundamentales de la captación de aguas subterráneas

Realizaremos una síntesis de los conceptos básicos de la hidráulica, así como también de sus aplicaciones; que serán de utilidad práctica.

Hidráulica

Es una rama de la física y la ingeniería que se encarga del estudio de las propiedades mecánicas de los fluidos, ya sean superficiales o subterráneos. Todo esto depende de las fuerzas que se interponen con la masa y el empuje de la misma

La particularidad de la hidráulica es que tiene carácter pluridisciplinar ya que engloba varias disciplinas de la física como son, la cinemática la estática,, la dinámica, que a su vez se estudian dentro de la mecánica convensional.

Aplicaciones de la Hidráulica

Actualmente las aplicaciones de la hidráulica son muy variadas, esta amplitud en los usos se debe principalmente al diseño y fabricación de elementos de mayor precisión y con materiales de mejor calidad, acompañado además de estudios mas acabados de las materias y principios que rigen la hidráulica y neumática. Todo lo anterior se ha visto reflejado en equipos que permiten trabajos cada vez con mayor precisión y con mayores niveles de energía, lo que sin duda ha permitido un creciente desarrollo de la industria en general.

Dentro de las aplicaciones se pueden distinguir dos: móviles e industriales.

o Aplicaciones Móviles: El empleo de la energía proporcionada por los fluidos a presión, puede aplicarse para transportar, excavar, levantar, perforar, manipular materiales, controlar e impulsar vehículos móviles tales como:

o Tractores.

o Grúas.

o Retroexcavadoras.

o Perforadoras, etc.

o Aplicaciones Industriales: En la industria, es de primera importancia contar con maquinaria especializada para controlar, impulsar, posicionar y mecanizar elementos o materiales propios de la línea de producción, para estos efectos se utiliza con regularidad la energía proporcionada por fluidos comprimidos. Se tiene entre otros:

o Maquinaria para la industria plástica

o Máquinas herramientas.

o Maquinaria para la elaboración de alimentos.

o Equipamiento para robótica y manipulación automatizada.

o Equipo para montaje industrial.

o Maquinaria para la minería.

o Maquinaria para la industria siderúrgica.

o La Hidráulica también nos ayuda a resolver problemas técnicos de cada una de

las siguientes especialidades:

o Aprovechamiento de captaciones de aguas subterráneas.- aplicados a la minería, la industria, la agricultura y usos de abastecimiento de agua potable.

o Aprovechamientos hidroeléctricos: Saltos o centrales hidroeléctricas, para cuya construcción son necesarias muchas y variadas obras hidráulicas.

o Aprovechamientos industriales: Circuitos hidráulicos existentes en diversas industrias, en otro tipo de centrales (térmicas convencionales, nucleares), e incluso en el interior de maquinaria no fundamentalmente hidráulica (motores, circuitos de refrigeración, etc.)

o Aprovechamientos sanitarios: Abastecimientos de agua potable y alcantarillado, tanto públicos como domiciliarios.

o Aprovechamientos agrícolas: Obras destinadas a proporcionar riego a extensiones de riego cultivable.

Flujo Hidráulico

El estado o comportamiento del flujo en un canal abierto es gobernado básicamente por los efectos de viscosidad y gravedad relativa a las fuerzas de inercia del flujo.

El flujo de un líquido en canales en general es con superficie libre, a diferencia del flujo en tuberías, que puede ser con superficie libre o bajo carga, lo que depende de si la conducción fluye llena o no. Para un flujo con superficie libre en tubería debe existir una superficie de líquido sometida a presión atmosférica.

Algunos factores que afectan el flujo de aguas en canales y conductos son:

· Caudal.

· Pendiente.

· Área de la sección transversal.

· Rugosidad de la superficie interior de la conducción.

· Condiciones de flujo (ej. en cañerías: lleno, parcialmente lleno, permanente, variado).

· Presencia o ausencia de obstrucciones, curvas, etc.

· Naturaleza del líquido, peso específico, viscosidad, etc.

Caudal

El caudal o gasto volumétrico es la cantidad de un líquido que pasa por unidad de tiempo a través de una sección de control. Es un parámetro que se encuentra presente en cualquier problema asociado con el intercambio de líquidos entre dos o más recipientes.

Su unidad de medida viene expresada por la relación de volumen por unidad de tiempo existiendo las siguientes equivalencias:

Q = Velocidad x Area = Volumen / tiempo

Es decir:

1 m3/hora = 1000 litros/hora = 0,277 litros/seg = 4,4 galones/minuto 1m3/seg = 3600 m3/h = 1000 litros/seg

Presión

Es el parámetro que relaciona a una fuerza por unidad de área sobre la cual actúa. Generalmente, para el tipo de problemas asociados a saneamiento, la presión que se utiliza esta medida respecto de la presión atmosférica, por lo que es la llamada presión relativa. A diferencia de la presión absoluta que tiene su punto de referencia en el vacío absoluto. Sabemos que un líquido en reposo o circulando a cielo abierto sometido a la presión atmosférica tiene una presión relativa igual a cero. Pero si medimos la presión absoluta esta sería de 1,02 bar ó bien 1,033 kg/cm2 (absolutos).

Altura Manométrica de una bomba

Relacionada con el concepto de altura de columna de líquido, expresa la energía de presión que una bomba debe aportar para elevar un líquido hasta alcanzar el nivel deseado. Su origen esta relacionado con la ecuación de Bernoulli que expresa el principio de conservación de la energía para todo fluido que circula en un conducto cerrado.

El término altura manométrica representa en esa ecuación la cantidad de energía que es necesario aportar a un kilogramo de líquido para que se cumpla el principio de igualdad energética cuando la energía entre dos puntos de control tomados arbitrariamente (a un lado y a otro de la bomba) no es la misma.

La unidad de medida es el metro, pero surge como derivación o simplificación del trabajo realizado por el líquido por unidad de peso de ese mismo líquido que escurre:

H bomba = kgm / kg = m

Altura de columna de líquido

Este parámetro que se encuentra directamente relacionado a la presión, nos dice cual sería la altura que alcanzaría una columna de líquido alojada dentro de un tubo vertical conectado a un conducto o recipiente presurizado. Al estar bajo presión, parte del líquido contenido en él sube por el tubo hasta ocupar una posición fija, en tanto no varía la presión. La altura de la columna de líquido es directamente proporcional a la presión dentro del recipiente e inversamente proporcional al peso específico.

Línea piezométrica

Es la línea que conecta los puntos a los que el líquido puede subir en distintos lugares a lo largo de la tubería o conducción, si se insertasen tubos piezométricos.

Es una medida de la altura de carga hidrostática disponible en distintos puntos; en el caso de agua que fluye por un canal, contrariamente a lo que ocurre con el flujo en una conducción bajo carga, la línea piezométrica se corresponde con el perfil de la superficie del agua.

Línea de energía

La energía total del flujo en cualquier sección respecto a una de referencia dada es la suma de la altura de elevación “z”, la altura de carga correspondiente a la altura de presión dinámica “V2/2g”. Generalmente a la pérdida de carga entre dos secciones se denomina hL.

Energía específica

La energía especifica o altura de carga es la suma de la altura piezométrica y la altura de presión dinámica “V2/2g”, medida respecto del fondo del canal. Este concepto de energía específica se usa en análisis de flujos en canales.

Flujo permanente

Un movimiento es permanente, cuando las partículas que se suceden en un mismo punto presentan, en este punto, la misma velocidad, poseen la misma densidad y están sujetas a la misma presión. Ósea, el flujo permanente tiene lugar cuando el caudal en cualquier sección transversal es constante.

Flujo uniforme y no uniforme

Existe flujo uniforme cuando el calado, área de sección transversal y otros elementos del flujo son constantes de sección a sección.

El flujo es no uniforme cuando la pendiente, el área de sección transversal y la velocidad, cambian de una sección a otra.

Ejemplo de flujo no uniforme permanente es el que atraviesa un tubo venturi para medidas de caudal.

Flujo variado

El flujo de un canal se considera variado si el calado cambia a lo largo del canal.

Nivel Estático

Es el nivel de agua presente en la formación acuífera antes de comenzar el bombeo. Este nivel se ve afectado por efectos meteorológicos (precipitación, infiltración) estacionales o por cargas adicionales (edificaciones), o por la descarga producida por pozos cercanos.

Nivel Dinámico

También llamada nivel de bombeo, por que es producido cuando comienza la descarga del acuífero por el pozo.

Este nivel depende del caudal de bombeo, del tiempo de bombeo y de las características hidrogeológicas del acuífero. También se debe tener en cuenta la técnica desarrollada en el diseño de pozo.

Abatimiento

Bajo condiciones de extracción o inyección de un pozo, la carga hidráulica inicial en cualquier punto del acuífero cambia. En condiciones de extracción de un pozo, la distancia vertical entre la carga hidráulica inicial en un punto en el acuífero y la posición baja de la carga hidráulica para el mismo punto es llamado abatimiento.

Para un acuífero libre el nivel del agua en el nivel freático está determinado por la distancia s(x,y,z,t), la cual es el abatimiento.

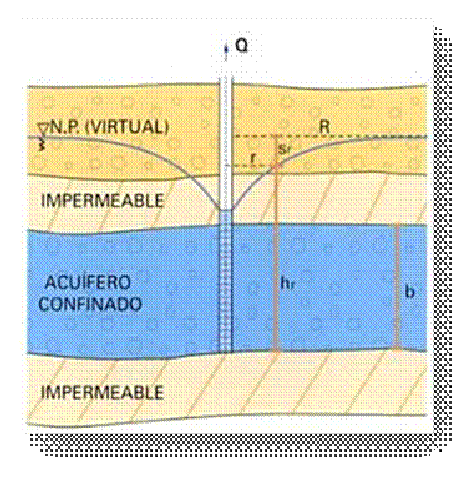
Para el caso del acuífero confinado, el abatimiento es definido con respecto a la superficie piezométrica. Este descenso de niveles, define la curva de abatimiento, por lo tanto es claro que el abatimiento presente su menor valor en lejanías del pozo y el mayor valor en el pozo. La dimensión del abatimiento es la longitud [L]. El abatimiento es generalmente expresado en metros de agua.

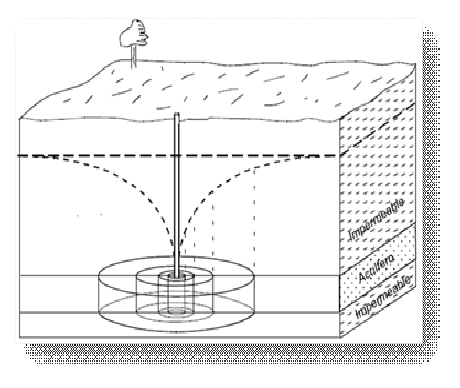
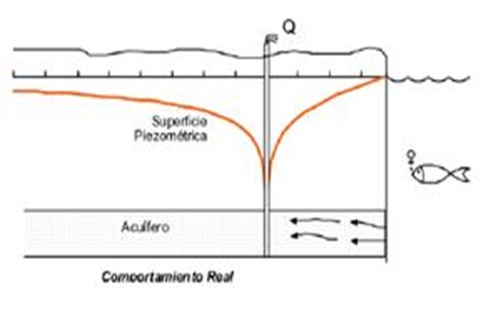
Esquema representativo del bombeo de un pozo.

Conos de Depresión (Conos de Descenso)

Forma tomada por el agua subterránea por su comportamiento cuando se bombea en un sondeo vertical. Al momento que empezamos a bombear en un acuífero libre cuya superficie freática inicial si fuse horizontal. El agua comienza a fluir radialmente hacia el sondeo, y, transcurrido un tiempo, la superficie freática habría adquirido la forma de un cono (figura siguiente), denominada cono de descensos. Esto puede apreciarse realmente si en los alrededores del sondeo que bombea existen otros sondeos para observación de los niveles.

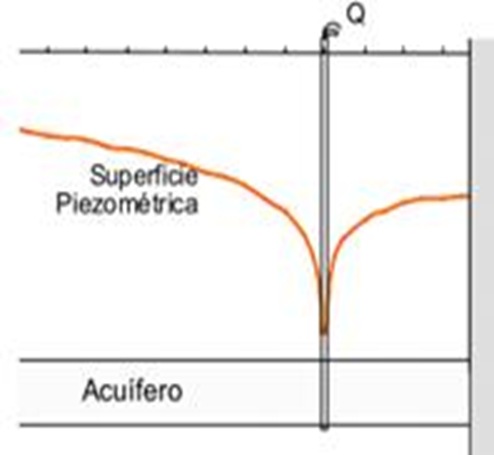
Cono de descenso alrededor de un sondeo bombeando.

Corte transversal del cono de depresión; la generatriz del cono corresponde a la ecuación S=f(r)

Al producirse el descenso del nivel estático del pozo, se establece un gradiente hidráulico entre cualquier punto de la formación y el pozo, originándose un movimiento radial desde todas las direcciones hacia el pozo en una forma simétrica y de tal manera que el caudal Q que se extrae del pozo es igual al caudal que pasa por cualquier sección del acuífero.

A medida que la velocidad aumenta mayor será el gradiente hidráulico ya que aumenta la fricción existente entre el fluido y las partículas sólidas en contacto; es por eso que lo que se forma alrededor del pozo se le conoce como cono de depresión que sobre un plano vertical presenta una curva conocida con el nombre de curva de abatimiento.

La forma convexa del cono se debe a que el agua que fluye radialmente hacia el sondeo tiene que atravesar cada vez secciones menores (las paredes de imaginarios cilindros concéntricos con el sondeo), de modo que, según Darcy, si disminuye la sección, tendrá que aumentar el gradiente para que el producto permanezca constante. Se denomina “desarrollo” a los trabajos posteriores a la perforación para aumentar el rendimiento de la captación, extrayendo la fracción más fina en materiales detríticos o disolviendo con ácido en calizas.

La forma, alcance y profundidad de este cono de depresión dependerá de las condiciones hidrogeológicas (coeficiente de almacenamiento y transmisividad del acuífero), del caudal y el tiempo de bombeo o inyección.

En el acuífero confinado el cono de depresión es la representación de la variación de los niveles piezométricos, en tanto que en el acuífero libre es además la forma real de la superficie piezométrica del nivel freático.

Captaciones de aguas subterráneas

Para extraer agua del terreno se utilizan diversos tipos de captaciones:

· Pozos Excavados

Es probablemente el tipo de captación más antiguo. En la actualidad se excava con máquinas y en rocas duras con explosivos. Sigue siendo la elección más adecuada para explotar acuíferos superficiales, pues su rendimiento es superior al de un sondeo de la misma profundidad. Otra ventaja en los acuíferos pobres es el volumen de agua almacenado en el propio pozo Diámetro= 1 a 6 metros o más Profundidad = generalmente 5 a 20 metros.

· Sondeos

Son las captaciones más utilizadas en la actualidad. Los diámetros oscilan entre 20 y 60 cm. y la profundidad en la mayoría de los casos entre 30-40 m. y 300 o más. Si la construcción es correcta, se instala tubería ranurada sólo frente a los niveles acuíferos, el resto, tubería ciega.

En acuíferos de muy poco espesor .Profundidad de 2 a 4 metros y longitudes de unas decenas a varios centenares de metros. Se excavan una o varias zanjas, que, siguiendo la pendiente topográfica, vierten a un pozo colector desde el que se bombea. Se utilizan tanto para explotación del agua subterránea poco profundas como para el drenaje necesario para la estabilidad de obras.

· Cono de descensos

El agua comienza a fluir radialmente hacia el sondeo, y, transcurrido un tiempo, por ejemplo unas horas, la superficie freática habría adquirido la forma que se presenta en la siguiente figura, denominada cono de descensos. Esto puede apreciarse realmente si en los alrededores del sondeo que bombea existen otros sondeos para observación de los niveles.

La forma convexa del cono se explica así: El agua que fluye radialmente hacia el sondeo tiene que atravesar cada vez secciones menores (las paredes de imaginarios cilindros concéntricos con el sondeo), de modo que, según Darcy, si disminuye la sección, tendrá que aumentar el gradiente para que el producto permanezca constante. Se denomina “desarrollo” a los trabajos posteriores a la perforación para aumentar el rendimiento de la captación, extrayendo la fracción más fina en materiales detríticos o disolviendo con ácido en calizas.

Cono de descensos en acuíferos confinados

En un acuífero libre, es la superficie freática la que toma la forma del cono de descensos. En cambio, si lo que se bombea es un acuífero confinado o semiconfinado, y suponemos que la superficie piezométrica inicial es horizontal, al iniciar el bombeo es dicha superficie la que forma el cono de descensos, y son igualmente válidas las consideraciones anteriores En ambos casos, libre y confinado, el agua circula radialmente hacia el sondeo, pero la diferencia es que en el acuífero libre el agua circula por toda la sección transversal, desde el cono hacia abajo, mientras que en el confinado solamente circula por el propio acuífero.

Cono de descensos en un acuífero confinado. Los cilindros concéntricos representan las superficies equipotenciales, cuya pérdida progresiva de energía queda reflejada en el cono formado por la superficie piezométrica.

Formas del cono según las características del acuífero

Si el acuífero tiene un mayor coeficiente de almacenamiento (S) o porosidad eficaz (me), los descensos serían menores, ya que el acuífero proporciona más agua, y por tanto el tama–o del cono sería menor.

Si el acuífero tiene una mayor transmisividad (T), la pendiente necesaria para que el agua circule será menor (de nuevo Darcy: q=K.gradiente; recordamos que T=K.espesor).

(a) A igual Transmisividad, el cono es mayor cuanto más bajo es el Coeficiente de Almacenamiento (o me). (b) A igual Coeficiente de Almacenamiento (o me), la pendiente del cono aumenta cuanto más baja es la Transmisividad

Fórmulas que expresan la forma del cono de descensos

Desde mediados del siglo XIX se intentó encontrar expresiones matemáticas que reflejaran la forma y evolución del cono de descensos. Es evidente la utilidad de estas expresiones en la práctica: podremos evaluar la influencia que tendrá un bombeo en puntos vecinos; si el radio de nuestro bombeo podría llegar a una zona determinada en la que se infiltra agua contaminada, o calcular si será preferible extraer el caudal necesario mediante un solo sondeo de mayor caudal o con varios de menor caudal, etc.

Observamos en la figura que la ecuación del cono ha de ser s=f(1/r) [s=descenso, r=distancia], es decir, a más distancia, menor descenso. Será función del caudal (Q): si bombeamos un mayor caudal generaremos un cono mayor.

En régimen variable, será además función del tiempo: s = f (1/r, t). En ambos casos, variable o permanente, será función del acuífero: mejor acuífero, menores descensos. Pero existe una diferencia fundamental: en régimen permanente, el acuífero ya no aporta agua por vaciado de poros (libre) o por descompresión (confinado), sino que solamente transmite el agua radialmente hacia el sondeo que bombea.

Por tanto, si se trata o no de un “buen acuífero” en régimen permanente dependerá de la transmisividad (T), mientras que en régimen variable dependerá de la transmisividad y del Coeficiente de Almacenamiento (S), que en un acuífero libre corresponde a la porosidad eficaz (me). En resumen, las fórmulas que reflejen la forma del cono han de ser así:

Régimen permanente: S = f (1/r, Q, 1/T)

Régimen variable: S = f (1/r, t, Q, 1/T, 1/S)

Supuestos Básicos

Las fórmulas más sencillas que nos expresan la forma del cono de descensos se refieren al caso más simple posible que reúne las siguientes características: - Acuífero confinado perfecto - Acuífero de espesor constante, isótropo y homogéneo - Acuífero infinito - Superficie piezomètrica inicial horizontal (=sin flujo natural) - Caudal de bombeo constante - Sondeo vertical, con diámetro infinitamente pequeño (=agua almacenada en su interior despreciable) - Captación “completa” (= que atraviese el acuífero en todo su espesor).

Posteriormente, las formulaciones básicas, válidas para esas condiciones ideales, se van complicando para adaptarse al incumplimiento de una u otra de las condiciones referidas: acuífero semiconfinado o libre, acuífero que se termina lateralmente por un plano impermeable.

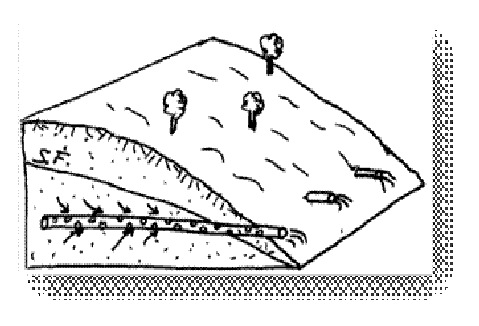
· Galerías

Ya existían galerías para agua en Mesopotamia en el siglo IV a. C. Con una ligera pendiente, el agua sale al exterior por gravedad, sin bombeo. Se excavan igual que en minería. En Canarias es la captación más frecuente, generalmente con varios km de longitud.

· Drenes

Similares a las galerías, pero son tubos de pequeño diámetro, perforados con máquina, normalmente hasta unas decenas de metros. Son más utilizados para estabilidad de laderas que para la utilización del agua.

· Pozos excavados con drenes radiales

Se utilizan en los mismos casos que los excavados pero con mayor rendimiento. Generalmente en buenos acuíferos superficiales cuando se requieren grandes caudales. Su radio equivalente puede evaluarse mediante la siguente fórmula (CUSTODIO, 1983, p.1823):

re = Radio equivalente

Lm = Longitud media de los drenes

n = Número de drenes

· Zanjas de drenaje

La resolución de la ecuación general de flujo

La ecuación general de flujo subterráneo es una ecuación diferencial en derivadas parciales de segundo orden que admite infinitas soluciones .Dicho de otro modo puede aplicarse a la inmensa mayoría de los de más sistemas hidrogeológicos, en concreto a todos aquellos a los que se pueda aplicar la ley de darcy

La resolución de un problema de concreto a partir de la ecuación general del flujo subterráneo exige las definiciones de las características particulares de ese sistema de flujo subterráneo, conocidas como sus definiciones de contorno, incluyendo su geometría (forma y dimensiones) y su relación con las unidades hidrogeológicas y otros elementos adyacentes

Existen tres tipos de contorno:

1.-Potencial impuesto, condición de contorno de primera clase o de dirichlet.

En este tipo de límite el potencial se conserva constante a lo largo del tiempo .Si el potencial es el mismo en todos los puntos del contorno, constituye una línea, una superficie equipotencial .suele estar asociado a contactos entre el acuífero y masa de agua de importancia: lagos, mares, ríos caudalosos, etc.

2.-Flujo impuesto, condición de contorno de segunda clase o de neumann.Existe un flujo de agua definido que sale del acuífero o penetra en el .Este flujo puede ser nulo en el caso del contacto entre el acuífero y una unidad impermeable .Las divisorias de agua también se ajustan a este tipo de condición de contorno

3.-Flujo condicionado por el valor del potencial hidráulico, condición de contorno de tercera clase o de cauchy .Se aplica a las entradas y salidas de agua del acuífero a través de capas semiconfinantes que lo separan de otra fuente de recarga externa .El flujo que sale del acuífero o penetra en el depende de la diferencia del potencial entre el acuífero y la fuente externa , de la conductividad hidráulica vertical del acuitardo o capa semiconfinante, de su extensión superficial y de su espesor

Una vez establecidas las correspondientes condiciones de contorno, la solución de la ecuación general del flujo es única y corresponde al problema que se plantea

La resolución de la ecuación general de flujo puede abordarse de tres maneras diferentes:

Ø Gráficamente

Ø Analíticamente

Ø Numéricamente

Si el nivel del agua no varía significativamente, las grandes masas de agua superficial(lagos, mares, embalses) pueden ser consideradas como condiciones de contorno de potencial constante. Foto: Embalso de camporredondo

· RESOLUCION DE LA ECUACION GENERAL DE FLUJO

La resolución grafica de la ecuación general del flujo solo es aplicable en régimen permanente (sobre representaciones graficas de la situación del acuífero en un tiempo determinado).Es conocida con el nombre de método de las redes de flujo

A.-Definición de la red de flujo

La ley de darcy permite definir un vector velocidad que es la resultante de todos los vectores que podrían definirse para cada uno de los poros en la zona considerada

Llamaremos línea de corriente a la línea que constantemente es tangente al vector velocidad defini9do en un medio poroso a partir de la ley de darcy .Matemáticamente seria la envolvente del vector velocidad .Una trayectoria seria una línea, más o menos tortuosa, que constituirá el lugar geométrica de las sucesivas posiciones de una partícula de agua en su movimiento a través de un medio poroso

B.-Superficies equipotenciales (en sistemas tridimensionales) o líneas equipotenciales (en sistemas uní o bidimensionales),son el lugar geométrico de los puntos que tiene el mismo potencial hidráulico. Se trata de superficies o líneas en las que el agua subterránea tiene la misma energía en todos sus puntos

C.-El gradiente geotérmico. Indica la dirección en la que se produce el máximo cambio de energía entre cada dos equipotenciales. Por lo tanto es perpendicular a los equipotenciales .Por lo tanto es perpendicular a las equipotenciales (camino más corto entre ellos). Como, según Ley de Darcy, el vector velocidad y el vector gradiente son paralelos entre si, el vector velocidad también seria perpendicular a las equipotenciales. Puede concluirse que líneas de corriente y equipotenciales son perpendiculares entre si .Para ello el medio ha de ser homogéneo e isótropo.

En un acuífero homogéneo e isótropo, líneas de corriente e equipotenciales constituyen una malla ortogonal que se llama red de flujo .la red de flujo define el movimiento de las aguas subterráneas puesto que las líneas de corriente van en la dirección perpendicular a las equipotenciales y en el sentido de los potenciales decrecientes

· Las redes de flujo

Permiten también el tratamiento cuantitativo del sistema hidrogeológico sin mas que aplicar la ley de darcy a la malla definida

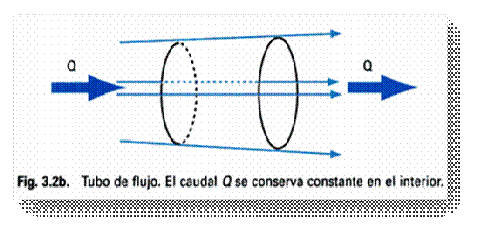
Se denomina tubo de flujo a la porción de acuífero limitada por una serie de líneas de corriente que pasan por un contorno cerrado .La propiedad esencial de los tubos de flujo es que el caudal que circula por ellos se conserva constante

Red de flujo en medio homogéneo e isotrópo: las líneas equipotenciales y de corriente son perpendiculares entre sí. Las líneas de corriente tienen el sentido de las potencias decreciones

Sea el tubo de flujo de la figura, definido por dos líneas de corriente en un sistema bidimensional homogéneo e isótropo de conductividad hidráulica K y en el que la distribución de energía del agua subterránea en su interior viene definida por las equipotenciales h₁ y h₂ , siendo h₁ > h₂

Aplicando la ley de Darcy se puede calcular el caudal circulante en la sección intermedia definida entre las dos equipotenciales

Este caudal será el mismo en cualquier sección del tubo de flujo perpendicular a las líneas de corriente. Si aumenta la sección disminuye la sección de flujo y viceversa, pero el caudal siempre es constante

A.-REDES DE FLUJO EN MEEDIOS HETEROGENEOS Y ANISOTROPOS

En medios heterogéneos hay que tener en cuenta que cuando una línea de corriente pasa de un medio de mayor conductividad hidráulica a otro de menor conductividad hidráulica, se refracta acercándose a la normal .Por el contrario cuando una línea de corriente pasa de un medio de menor conductividad hidráulica a otro de mayor conductividad hidráulica, se refracta alejándose de la normal (Hubbert, 1940). Cuantitativamente puede expresarse

En la practica, partiendo de un medio heterogéneo y anisótropo, se puede llegar a un medio homogéneo e isótropo realizando una serie de transformaciones no muy complicado .Una vez obtenido el medio homogéneo e isótropo equivalente se puede trazar en el la red de flujo y realizar su interpretación cualitativa y cuantitativa .los resultados obtenidos se puede aplicar directamente al medio original.

Transformación de un medio heterogéneo y anisótropo en un medio homogéneo y anisótropo

Un medio heterogéneo y anisótropo puede representarse por “n” unidades, estratificadas anisótropas y de diferentes características de conductividad hidráulica cada una de ellas.

Transformar este medio en homogéneo y anisótropo exige calcular una conductividad hidráulica vertical equivalente a las n verticales y una conductividad hidráulica horizontal equivalente a las n horizontales.

Empecemos por calcular la conductividad hidráulica vertical equivalente. Para ello hacemos circular un caudal Q conocido en la dirección de la conductividad hidráulica vertical a través de una sección A igual para todo el conjunto de unidades hidrogeológicas.

“Calculo de la permeabilidad vertical equivalente”

La perdida de energía total que experimenta el agua al atravesar el conjunto de unidades es la suma de la energía que pierde al atravesar cada una de ellas.

De la Ley de Darcy se tiene:

Donde:

: Es la pérdida total de energía

: Es la suma de los espesores de cada una de las capas de la muestra

Q: Es el caudal circulante

A: es la sección normal al flujo

K: es la conductividad hidráulica vertical equivalente

La pérdida de energía en cada de una de las unidades hidrogeológicas será:

Sumando:

Con lo cual la conductividad hidráulica vertical equivalente seria:

Para el cálculo de la conductividad hidráulica horizontal equivalente se hace circular el agua en la dirección horizontal y se aplica, como en el caso anterior la Ley de Darcy.

En este caso el agua experimenta la misma perdida de energía en su recorrido por cualquiera de las capas que integran el medio. El caudal total circulante horizontalmente, a través del medio será:

Siendo:

Q: Caudal circulante en la dirección horizontal

a: Anchura de las capas (la misma para todas)

b: Espesor saturado total (suma del espesor saturado de todas las capas)

: Conductividad hidráulica horizontal equivalente

: Perdida de energía (la misma para todas las capas).

: Camino recorrido por el flujo subterráneo

“Calculo de la permeabilidad horizontal equivalente”

El caudal circulante por la primera capa sería:

En donde b₁ es el espesor saturado, y k₁ la conductividad hidráulica de la primera capa.

El caudal circulante por la segunda capa sería:

En donde b₂ es el espesor saturado, y k₂ la conductividad hidráulica de la segunda capa.

Y por la capa n:

En donde b_n es el espesor saturado, y k_n la conductividad hidráulica de la enésima capa.

La suma de todos estos caudales será el caudal total:

Y la conductividad hidráulica horizontal equivalente será:

Soluciones analíticas de la ecuación general del flujo

La resolución analítica de la ecuación general del flujo es uno de los temas a los que se presta mayor atención en la investigación hidrogeológica a partir del trabajo de Darcy (1856). Quizá el primer trabajo que se basa en la Ley de Darcy, para el estudio del movimiento del flujo de agua hacia un pozo perforado en un acuífero libre, sea el de Dupuit (1863), Forchheimer (1886) y Slichter (1899), independientemente llegan a la ecuación general del flujo para régimen permanente a partir del principio de conservación de la masa y la Ley de Darcy. Jacob (1940), y posteriormente Cooper (1966), deducen la ecuación general del flujo para régimen transitorio.

Establecida la ecuación general del flujo subterráneo para régimen estacionario y no estacionario, los primeros trabajos de investigación en la determinación de soluciones particulares están relacionados con el movimiento del agua subterránea hacia pozos, captaciones de aguas subterráneas por excelencia.

Conviene señalar que la aplicación de una ecuación matemática al medio natural exige una simplificación importante que implica la aceptación de las siguientes hipótesis de partida:

En cuanto al acuífero:

Ø Homogeneidad e isotropía en toda su extensión, que se supone infinita.

Ø Coeficiente de almacenamiento constante.

Ø Muro horizontal y espesor constante.

Ø El acuífero es, en todo momento y en todo lugar libre, confinado o semiconfinado.

En cuanto al flujo subterráneo:

Ø Es válida la Ley de Darcy.

Ø No hay flujo natural, es decir la superficie piezométrica inicial es un plano horizontal.

Ø Una vez iniciado el bombeo el flujo es radial y horizontal (convergente hacia el pozo si el caudal es de extracción y divergente desde el pozo si el caudal es de inyección). Esto implica que las superficies equipotenciales sean cilindros verticales concéntricos con el pozo de bombeo.

Ø No existen perdidas de energía por rozamiento al penetrar el agua en el pozo.

Ø El descenso en el infinito es cero.

En cuanto al pozo de bombeo:

Ø Esta ranurado a lo largo de todo el acuífero, al que corta en su totalidad.

Ø El caudal de bombeo es constante a lo largo del tiempo.

Ø El pozo considerado es el único que bombea en el acuífero.

Ø El radio del pozo es lo suficientemente pequeño como para poder suponer que el agua almacenada en el pozo no influye en el caudal de bombeo.

Ø La variación del nivel piezométrico consecuencia del bombeo es simultanea a la extracción (o inyección) de agua y proporcional al volumen extraído (ó inyectado).

En cuanto al agua:

Ø Tiene densidad y viscosidad constantes en el espacio y en el tiempo.

Aceptando estas hipótesis, considerando que el régimen del acuífero puede ser estacionario o no estacionario y las condiciones de contorno propias de acuífero confinado, semiconfinado o libre, se llega para cada caso a una solución analítica de la ecuación general del flujo, que es la ecuación de la superficie piezométrica en el entorno del pozo para unas determinadas condiciones de bombeo.

A partir de ahora se supondrá el caso de caudales de extracción (positivos) por ser el más frecuente. En el caso de caudales de inyección la formulación es la misma, solo cambia el signo del caudal y pasan los descensos a ser negativos, es decir, se convierten en ascensos sobre el nivel piezométrico inicial.

Se establece, al objeto de medida de magnitudes, un sistema de ejes cartesianos cuyo eje de ordenadas es el eje del pozo y el de las abscisas el muro del acuífero.

Las unidades de medida han de ser homogéneas.

Las expresiones que se exponen a continuación tienen un doble uso:

· Conocidos los parámetros hidrogeológicos del acuífero se puede conocer el efecto del bombeo en cualquier punto del mismo para diversos caudales de extracción.
Se incluye en este aspecto el cálculo de la distancia a partir de la cual el efecto del bombeo es nulo, conocida como radio de influencia del bombeo.
También puede determinarse el caudal específico del pozo, que es una medida de su rendimiento. Se expresa como el caudal de extracción dividido por el descenso producido por el bombeo una vez estabilizado el nivel en el pozo a efectos prácticos. El caudal específico es directamente proporcional a la transmisividad del acuífero.
Conocidos los efectos puntuales de la extracción de un determinado caudal en un pozo, determinar los parámetros hidrogeológicos del acuífero. A este proceso se le suele conocer con el nombre de ensayo de bombeo.

· El agua al penetrare en el pozo sufre un rozamiento “extra” con los elementos relacionados con el pozo y su construcción: empaque de gravas, filtro, resto de lodos de perforación, etc.

Este rozamiento lleva consigo una pérdida de energía que se conoce con el nombre de pérdidas de carga, que implica que el descenso medido en el propio pozo de bombeo sea mayor que el que teóricamente se obtendrá aplicando la ecuación correspondiente. Esto hace que, si se considera el pozo de bombeo como punto para medir descensos, los valores medidos se apartan de los teóricos tanto más cuanto mayores sean las pérdidas de carga( cuanto peor hecho esté el pozo) quedando falseados los valores de los parámetros obtenidos de esta manera.

Existen en la actualidad números programas informáticos parta la interpretación automática de ensayos de bombeo. Un método de interpretación, basado en hojas electrónicas de cálculo, de uso libre, es el desarrollado en el USGS por Halford y Kuniansky (2002).

Concepto de régimen permanente

Acuífero confinado en régimen permanente:

La siguiente figura muestra un esquema de los factores que intervienen en la ecuación de Thiem, cuya expresión es:

Donde:

· S_r es el descenso en el nivel piezométrico que se produce a una distancia r del pozo de bombeo [L].

· T es la transmisividad del acuífero [L² T^-1].

· Q es el caudal de bombeo [L³ T^-1].

· R es el radio de influencia [L].

Pozo en acuífero confinado en régimen permanente (Thiem).

Esta ecuación, conocida como la formula de Thiem (1906), permite obtener, conocidos el radio de influencia y la transmisividad del acuífero, el descenso que produciría en un punto situado a una distancia determinada del pozo, la extracción de un determinado caudal. Dicho de otra manera, proporciona la ecuación del cono de bombeo (descensos en función de la distancia), producido por la extracción a partir de un pozo de un determinado caudal de agua.

Acuífero semiconfinado en régimen permanente: Ecuación de De Glee (1930)

La figura siguiente muestra el esquema de funcionamiento correspondiente a un acuífero semiconfinado en régimen permanente.

Pozo en acuífero semiconfinado en régimen permanente (De Glee).

El acuífero esta conectado hidráulicamente a una fuente externa capaz de proporcionar o recibir agua manteniendo su nivel constante a efectos prácticos. El bombeo se inicia en estado de equilibrio (la fuente de recarga y el acuífero tienen el mismo nivel piezométrico). Al comenzar el bombeo desciende el nivel piezométrico en el acuífero y, como consecuencia, comienza hacia él un flujo vertical regulado por la Ley de Darcy, desde la fuente externa a través del acuitardo.

El sistema tiende a un nuevo estado de equilibrio en el que toda el agua extraída del acuífero por el bombeo del pozo procederá de la fuente de recarga a través del acuitardo. A partir de este momento se alcanza el régimen estacionario en el que los potenciales hidráulicos son constantes a lo largo del tiempo. La deformación de la superficie peizométrica del acuífero viene dada por la ecuación de De Glee (1930).

Donde:

S_r = descenso estabilizado [L], producido a una distancia r, [L], del eje del pozo al bombear un caudar Q [L³ T^-1].

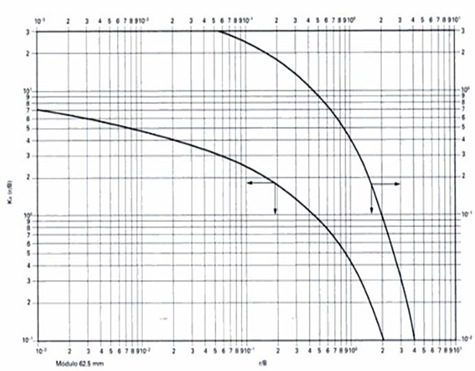
K₀ (r/B)= función del pozo (ábaco de De Glee).

= factor de goteo [L].

T = transmisividad del acuífero [L² T^-1].

K´= conductividad hidráulica vertical del acuitardo [LT^-1].

b`= potencia del acuitardo [L].

Abaco de Glee

Para obtener lo parámetros hidrogeológicos del acuífero y del acuitardo puede procederse de la siguiente manera:

Tomando logaritmos:

Puede apreciarse que so a log K₀ (r/B) se le suma una constante se obtiene log s y que si a log r se le resta una constante se obtiene log (r/b)

Así pues, si en un ensayo de bombeo, una vez alcanzado el régimen permanente, se mide el descenso producido a varias distancias del pozo de bombeo, obtendremos una serie de puntos [(r₁, s₁ … (r_{n ,} s_n ))], que representados en papel biologarítmico, darán lugar a una gráfica exactamente igual a la de De Glee pero desplazada de ella por una traslación.

Superponiendo ambas gráficas, conservando los ejes paralelos, y seleccionando un eje común a ambas (no hace falta que el punto esté sobre la línea que define las gráficas, puesto que una vez superpuestas la traslación se ha verificado en todo el semiplano), se pueden obtener los valores numéricos (se usan negritas para identificar que se trata de valores numéricos) de las coordenadas del punto seleccionado en ambas gráficas: s, r, K₀ (r/B) y (r/B). Las coordenadas así medidas se diferencian entre sí en el valor de la traslación y por lo tanto deben satisfacer la ecuación de De Glee

Como el caudal es conocido puede determinarse la transmisividad del acuífero.

Por otra parte:

De donde puede obtenerse el valor de B. conocido B, como la transmisividad ya es conocida puede calcularse k´/b´y de aquí k´, conductividad hidráulica vertical del acuitardo, se de alguna manera (por ejemplo, a partir de la columna litológica del sondeo), se conoce b´, potencia del acuitardo.

EJEMPLO: se realiza un ensayo de bombeo en un acuífero semiconfinado por el techo por un acuitardo de 10 metros de espesor. Se bombea desde un pozo totalmente penetrante en el acuífero en un caudal constante de 100 L/s. una vez estabilizado el cono de bombeo se miden descensos en piezómetros situadas a las distancias indicadas a continuación. Se pide calcular la transmisividad el acuífero y la conductividad eléctrica vertical del acuitardo.

Ensayo de bombeo en acuífero semiconfinado en régimen permanente (método de De Glee)

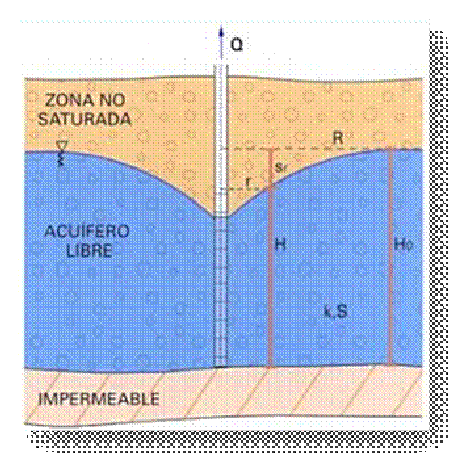
Acuífero libre en régimen permanente: ecuación de Dupuit

Una vez estabilizado el cono de bombeo como se muestra en la figura el espesor saturado del acuífero será mínimo en el pozo de bombeo y máximo a partir de una distancia equivalente al radio de influencia del bombeo. Por esta causa, en la zona del acuífero afectada por el bombeo, la transmisividad el acuífero variará espacialmente dependiendo de la magnitud del espesor saturado, siendo máxima con el máximo espesor saturado y mínima con el mínimo espesor saturado. Al ser el acuífero homogéneo e isotrópico la conductividad hidráulica no varía de un punto a otro ni de una a otra dirección.

Pozo en acuífero semiconfinado en régimen permanente (Dupuit).

Por otra parte, al ser la superficie freática una superficie física, las líneas de corriente pierden la horizontalidad en el entorno próximo del pozo condicionando su dirección a la forma del cono de bombeo. Debido a esto, en esta zona afectada por el bombeo las superficies equipotenciales, perpendicularmente a las líneas de corriente, no son cilindros verticales.

Si los descensos producidos por el bombeo son muy pequeños en comparación con el espesor saturado del acuífero, pude asumirse el error de considerar la transmisividad constante del flujo horizontal, y aplicar entonces la ecuación de Thiem (1906).

Si no es posible asumir descensos despreciables en comparación con el espesor saturado del acucífero, se aplica la ecuación conocida como aproximación de Dupuit:

Donde:

· H0 es el espesor saturado del acuífero antes de comenzar el bombeo, que coincide con el valor del potencial hidráulico en el acuífero [L].

· H es el potencial hidráulico a una distancia r [L] del eje del pozo una vez estabilizado el cono de bombeo [L].

· Q es el caudal constante de bombeo [L³ T^-1].

· K es la conductividad hidráulica del acuífero [LT^-1].

· R es el radio de influencia del bombeo [L].

Ensayo de bombeo en un pozo de un acuífero semiconfinado en régimen permanente (método Dupuit)

Donde:

· S es el descenso [L] que se produce a una distancia r [L] de un pozo que bombea un caudal constante q durante un tiempo t [T], en un acuífero confinado de transmisividad T y coeficiente de almacenamiento S.

· W (u) es la función de pozo. (ábaco de Theis)

Tomando logaritmos:

Ábaco de Theis

Es decir, que si a log W (u) se le suma una constante se obtiene log s y si a log t se le suma una constante se obtiene log (1/u).

Por lo tanto, si en un papel bilogarítmico representamos descensos en función del tiempo, medido a una distancia r del pozo de bombeo, obtendremos una gráfica idéntica a la del ábaco de Theis aunque desplazada de ella por una traslación de ejes de valor determinado por las constantes antes dichas.

Suponiendo las curvas de ambas gráficas, manteniendo paralelos los ejes, se puede seleccionar un punto común cuyas coordenadas, referidas a los ejes de ambas gráficas, llevan implícita la traslación y proporcionan los correspondientes valores numéricos de W (u), 1/u, s y t, que ha de satifacer la ecuación de Theis, pudiéndose escribir:

De donde puede obtenerse la transmisividad. Conocido el valor de este parámetro:

Y se calcula el coeficiente de almacenamiento.

Conocidos los valores de T y S, pueden calcularse los descensos para cualquier distancia y tiempo de bombeo, conocido el caudal de bombeo.

Análogo razonamiento puede realizarse para el caso de considerar descensos en función a la distancia, aunque en este cado seria necesario definir para un tiempo determinado el descenso producido en varios puntos, al objeto de poder definir bien la gráfica siendo necesario contar, además de con el pozo de bombeo, con varios puntos de medida situados a distancias diversas del de bombeo.

Concepto de régimen no permanente

Acuífero Confinado en Régimen Transitorio. Ecuación de Cooper y Jacob (1946):

Para el caso de que µ < 0.05 puede aplicarse la simplificación logarítmica de Cooper y Jacob (1946) y Jacob (1950).

Desarrollando el logaritmo, tenemos:

Es decir, representando en papel semilogarítmico (s en la escala aritmética y t en la escala logarítmica) la ecuación de Cooper – Jacob es un recta pendiente positiva:

Y de ordenada en el origen (Fig. 3.21):

De la gráfica semilogarítmica puede deducirse la pendiente de la recta como:

Si se elige una abscisa en la que el cociente entre los tiempos sea 10 (tiempos diferentes entre sí en un módulo logarítmico), se puede poner la pendiente de la recta como:

Y de ahí obtener T. Conocida la transmisividad y sabiendo que cualquier punto de la recta satisface la ecuación de Cooper – Jacob, bastaría obtener de la gráfica cualquier par (t_i + s_i), llevarlo a la ecuación y sacar el valor de S.

Para facilitar los calculos se escoge como punto a introducir en la ecuación el correspondiente al tiempo (t_o) que hace que el descenso sea cero. Quedará:

Por lo que ha de ser:

O:

De donde puede obtenerse el coeficiente de almacenamiento. El tiempo se obtiene prolongando la recta hasta cortar el eje de abscisas.

Al igual que en el caso de la solución de Theis podrían medirse, para un determinado tiempo, descensos en puntos situados a distancias conocidas del pozo de bombeo, y una vez obtenida la recta seguir una metodología análoga a la explicada.

Para definir la recta serían necesario al menos dos puntos de medida además del pozo de bombeo.

Por analogía entre las ecuaciones de Thiem y de Cooper – Jacob puede deducirse que en este caso el radio de influencia, R:

Es decir, si a:

Se le suma una constante:

Se obtiene log s. Si a log t se le suma una constante:

Se obtiene log (1/µ).

Bastará representar en papel bilogarítmico los descensos medidos en función del tiempo y superponer la gráfica obtenida a la de la función de pozo, conservando los ejes paralelos, para obtener el valor de la traslación. A las curvas superpuestas les corresponde un valor de (r/B) en la gráfica de la función de pozo (Walton 1960, 1962) (Fig. 3.23).

Superpuestas las gráficas se obtienen los valores numéricos de las coordenadas de un punto común referidos a ambas gráficas: W (u, r/B), 1/u, s y t, y puede ponerse:

De donde puede despejarse T. Conocida la transmisividad se puede obtener el coeficiente de almacenamiento del acuífero de:

Se obtiene B y de ahí el valor del cociente k´/b´. Y si de la columna litológica del pozo puede saberse el valor del espesor del acuitardo, es posible conocer su conductividad hidráulica vertical.

Conocidos todos los parámetros es posible calcular, para cualquier caudal constante de bombeo, los descensos producidos a cualquier distancia del pozo al cabo de un determinado tiempo de comenzar el bombeo.

Acuífero Libre en Régimen Transitorio. Ecuación de Neuman (1975):

Cuando se bombea un acuífero libre sin alcanzar la estabilización del cono de bombeo, el espesor saturado del acuífero varia en el espacio y en el tiempo. Encontrar una ecuación capaz de admitir esta doble variación es un problema que no está resuelto.

En la práctica, cuando los descensos producidos por el bombeo son pequeños en comparación con el espesor saturado del acuífero, puede asumirse que la transmisividad es constante en el espacio y en el tiempo y aplicar la ecuación de Theis.

También puede recurrirse a prolongar el bombeo en el tiempo hasta que los descensos sean tan pequeños que pueda asumirse el régimen casi permanente y aplicar entonces la ecuación de Dupuit. Esta metodología tiene el inconveniente de que permite calcular la conductividad hidráulica pero no el coeficiente de almacenamiento.

En el primer caso se trata de una aproximación que a veces puede resultar un tanto burda, puesto que la extracción de agua de un acuífero libre supone un vaciado físico del acuífero en el que interviene el drenaje por gravedad, que es un fenómeno lento.

No es aceptable, entonces, la hipótesis de que el agua se libera, en el acuífero, instantánea y simultáneamente a la extracción, dejando de cumplirse el modelo de Theis.

Neuman (1975), establece la siguiente ecuación para el caso del acuífero libre en régimen transitorio con descensos pequeños con respecto ala espesor saturado del acuífero:

Donde:

S es el espesor [L] que se produce a una distancia r [L] del pozo que bombea un caudal constante Q [L³T^-1], durante un tiempo t [T].

W (u_A, u_B, r) es la función de pozo (Neuman 1975).

El método de Neuman asume que en los primeros momentos del bombeo el agua se libera instantáneamente del almacenamiento del acuífero como consecuencia de fenómenos elásticos. El acuífero se comporta como confinado de transmisividad T y coeficiente de almacenamiento S y sigue, por lo tanto, la ecuación de Theis con µ_A en la función de pozo.

Pasados esos momentos iníciales, cuya dirección puede ser de escasos minutos, comienza a llegar al cono de bombeo un flujo vertical de agua procedente del drenaje por gravedad de los poros del acuífero (fenómeno lento para el que no puede aceptarse la hipótesis de que el agua se libera del acuífero instantáneamente y al mismo tiempo en el que se produce el bombeo).

Este drenaje diferido implica una amortiguación en los descensos, curvas tipo A, y un alejamiento del modelo de Theis. Finalmente en una tercera etapa, después de un tiempo largo de bombeo, el drenaje diferido disminuye sensiblemente y las gráficas tiempo descenso tienden de nuevo al modelo de Theis con u_B en la función de pozo, en la que ya interviene el coeficiente de almacenamiento característico de los acuíferos libres, m_e.

En la practica se realiza un ensayo de bombeo a caudal constante midiendo descenso en función del tiempo en un punto situado a una distancia r, conocida, del pozo de bombeo. Hay que ser diligentes en las primeras medidas para poder obtener los tramos segundo y tercero. A este efecto conviene previamente, utilizando valores esperables de los parámetros hidrogeológicos del acuífero, calcular, al menos en una primera estimación, el orden de magnitud del tiempo de duración del ensayo.

En segundo lugar se representan en papel bilogarítmico los valores de los descensos en función del tiempo. La escala logarítmica debe tener el mismo modulo que el ábaco de Neuman.

A continuación, conservando siempre paralelos los ejes de ambos gráficos, se superpone el primer tramo de la gráfica de campo al ábaco de Neuman en la zona de curvas tipo A y se obtiene el valor r. Además se obtienen los valores numéricos de las coordenadas de un punto común con respecto a los ejes de ambas gráficas s, t, 1/u_A y W.

Con estos datos:

Válido para los primeros momentos del bombeo.

Después se procede al ajuste de la grafica de campo con al curva del ábaco del mismo valor de r, pero ahora en la zona de las curvas tipo B correspondientes a los tiempos finales del bombeo. De manera análoga al caso anterior se obtienen los valores numéricos de las coordenadas de un punto común con respecto a los ejes de ambas gráficas s, t, 1/u_A y W, y de nuevo:

Válido para los momentos finales del bombeo.

Si el ensayo de bombeo esta bien realizado y la metodología bien aplicada, los valores de transmisividad obtenidos de uno u otro modo deben ser muy semejantes.

La conductividad hidráulica horizontal del acuífero puede calcularse como:

Siendo b el espesor saturado antes del comienzo del bombeo de:

Puede obtenerse la conductividad hidráulica vertical del acuífero K_v [LT^-1].

Si los descensos son significativos con relación al espesor saturado, Neuman sugiere efectuar sobre ellos la siguiente corrección antes de aplicar la metodología expuesta:

Siendo s_c el descenso corregido, s el descenso medido, y b el espesor saturado en el acuífero medido antes de comenzar el bombeo.

Transiciones y Límites de los Acuíferos:

Principio de superposición e interferencia de pozos

DEFINICION.- Este principio, se encarga de analizar la interferencia entre una batería de pozos en una formación acuífera, y el efecto que presenta este en la producción de los mismos. El principio de superposición nos permite calcular descensos cuando el caudal es variable. Por ejemplo, supongamos que en un acuífero de características conocidas se ha bombeado durante 15 horas: las 10 primeras, un caudal de 4 litros/seg , y las 5 horas siguientes se aumenta el caudal a 7 litros/seg.

Como en la realidad, se Encuentran los acuíferos con limitaciones hidrogeológicas definidas, que restringen la aplicabilidad de los métodos analíticos, que suponen la extensión infinita de los acuíferos, como lo muestra las Figuras

El método de las imágenes se utiliza para resolver teóricamente estos casos, aproximando una extensión finita de los acuíferos, con un pozo real y otro imagen. Basado en la linealidad de la Ecuación de Laplace (Para acuíferos libres, se mantiene si sí la variable de estado es h₂ y no h₁), suponiendo el trabajo de cada pozo y luego superponerlos, para así obtener la resultante de todos los pozos trabajando en conjunto.

El efecto producido en la superficie freática o piezométrica por dos o más pozos que bombean (o inyectan) es el mismo que la suma de todos los efectos que habrían producido cada uno de los pozos individualmente, como si los otros no existieran. Es más sencillo explicarlo con un ejemplo: Supongamos que deseamos saber el descenso generado en el pozo X por los sondeos en A y en B con las características indicadas en la figura.

Si disponemos de los datos suficientes para calcular el descenso que produciría A si B no bombeara, y análogamente el que produciría solamente B, en el caso real (bombean los dos) bastará calcular el descenso producido por uno y por otro y sumarlos. Para que los cálculos sean lo más simples posibles, supongamos que el ejemplo de la figura se desarrolla en un acuífero confinado perfecto. Primero aplicamos la ecuación de Jacob1 para obtener el descenso producido por A:

Después calculamos el descenso producido por B, y después sumamos ambos descensos

Representando los descensos a lo largo del plano que une A y B observamos el cono generado por A, el generado por B (en rojo) y la suma de ambos, que sería lo observado en la realidad. Para el cálculo se han utilizado los datos del ejemplo anterior, suponiendo que la distancia entre A y B es de 200 metros.

El Principio de Superposición se define y utiliza en varios campos de la Física, especialmente para la superposición de ondas. A lo largo de todo el tema utilizamos la ecuación de Jacob (acuíferos confinados) porque es la más simple. Por supuesto, en todos los ejemplos habría que aplicar la ecuación correspondiente (acuífero semiconfinado, libre...)

· Bombeo con caudal variable

Para ello, podemos suponer que en el mismo sondeo están funcionando dos bombas: una mantiene el caudal de 4 litros/seg hasta el final, y a las 10 horas, la segunda bomba, introducida en el mismo sondeo comenzara a extraer 3 litros/seg (el incremento de caudal que realmente se produjo). Esta ficción tiene que producir el mismo efecto que la realidad, puesto que las últimas 5 horas se bombeaban 4+3= 7 litros/seg.

También es sencillo simular una disminución de caudal. Supongamos que en un caso similar al anterior, el caudal disminuye de 9 litros/seg a 7. Bastará suponer que el caudal de 9 permanece constante, y que una segunda bomba comienza a inyectar un caudal de 3 (por tanto, -3 litros/seg), como se esquematiza en la figura siguiente:

Recuperación También puede plantearse el caso de que deseemos conocer los descensos existentes después de un tiempo τ (t griega, tau) de bombeo y de un tiempo t de descanso. Supongamos que el sondeo estuvo bombeando 10 litros/seg durante 3 horas, después se detuvo, y ha estado 2 horas parado. Se desea conocer el descenso después de esas 2 horas de descanso. Basta suponer (de nuevo la imagen de las dos bombas en el mismo sondeo) que el bombeo no se interrumpió, sino que a esa misma hora comenzó a inyectarse el mismo caudal que se está extrayendo. Es obvio que extraer 10 litros/seg y simultáneamente inyectar 10 litros/seg sería lo mismo que no extraer nada. Con las cifras de la figura adjunta, bastaría aplicar la fórmula correspondiente dos veces: 1º) Q=10 litros/seg y tiempo=5 horas, 2º) Q= –10 litros/seg y tiempo=2 horas. Finalmente, sumar los valores obtenidos por ambos cálculos.

A.-Sondeos que inyectan agua: Conos de ascensos Sabemos que si inyectamos un caudal se genera un cono de ascensos idéntico al que se hubiera creado al bombear el mismo caudal, pero invertido. Para calcularlo es suficiente utilizar la fórmula adecuada al tipo de acuífero de que se trate, simplemente introduciendo en la fórmula un valor negativo para el caudal, con lo que la fórmula nos devuelve un descenso negativo, es decir: un ascenso Esta idea general es válida para cualquier acuífero: sólo habría que aplicar las fórmulas adecuadas a acuíferos semiconfinados o libres. Pero vamos a ver aquí brevemente la aplicación a acuíferos confinados, que siempre es lo más simple.

En la figura adjunta vemos los descensos en un acuífero confinado que estuvo bombeando 3 horas tras las cuales ha estado detenido otras 2 horas 2

En la figura se han señalado descensos a los 240 minutos, cuando llevaba parado 1 hora: Si el bombeo no se hubiera detenido (hubiera bombeado 4 horas) el descenso alcanzado hubiera sido de La virtual inyección de un caudal idéntico al bombeado,

tras 1 hora, habría generado un ascenso Sr. Por tanto, el descenso residual es:

El cálculo con la fórmula de Jacob sería:

Si conocemos solamente un dato de descenso residual (s’) tras un tiempo de recuperación t, y el caudal (Q), podemos utilizar la expresión anterior para evaluar la transmisividad (T) del acuífero.

Ejemplo: Se ha bombeado un caudal de 5 litros/seg durante 2 horas. Se detiene el bombeo y 1,5 horas después, el descenso residual es de 0,93 m. Calcular la Transmisividad. Despejando T en la última fórmula, resulta:

Mucho más fiable es disponer de todos los datos de la recuperación y representar s’ en función de Log (τ + t / t). El cálculo de T es muy sencillo, por el mismo procedimiento que la práctica del método de Jacob. Ejemplo: Se ha bombeado un caudal de 3,5 litros/seg durante 3 horas (τ ), y tras la detención del bombeo se han medido en un piezómetro próximo los tiempos y descensos residuales que se indican en las dos primeras columnas de la tabla adjunta: Calculamos la tercera columna, (t+τ)/ t. Por ejemplo, para 5 minutos será: (5+180)/5

El gráfico se ha calculado con la fórmula de Theis y con los siguientes datos: T=100 m2/día, S= 5.10-5, Q= 10 litros/seg, r= 50 m

Representamos en un gráfico semilogarítmico los descensos residuales en funcion de (t+τ)/ t: Si aplicamos la ecuación (1) a dos puntos de la recta de modo que en abcisas uno sea 10 veces mayor que el otro, y restamos miembro a miembro, resulta (ver la figura adjunta): Con los datos del grafico adjunto leemos que para una variación en abcisas de 2 a 20, el incremento en ordenadas es 3,4 metros. Aplicando la fórmula anterior, resulta:

B.- Teoría de las Imágenes.- Cuando el acuífero termina lateralmente mediante un plano que pueda asimilarse más o menos a un plano vertical y rectilineo, puede aplicarse la Teoría de las Imágenes, también basad en el Principio de Superposición.

El plano límite puede ser de dos tipos: borde negativo (barrera impermeable) o borde positivo (un lago o río, cuyo nivel no se ve afectado por el bombeo). Analicemos primero el caso de un borde negativo o impermeable. Si una situación de este tipo se produce en la realidad, el cono nunca es simétrico, sino que baja más por el lado del borde impermeable, ya que por ese lado le llega menos agua. La Teoría de las Imágenes en este caso podría enunciarse así: Los descensos generados por un sondeo en un acuífero limitado por un borde negativo son los que se producirían si el acuífero fuera ilimitado, pero que existiera otro sondeo idéntico al que bombea reflejado por el borde negativo que actúa como un plano de simetría .

En la figura de la derecha observamos cómo podemos generar el cono observado en la realidad mediante la superposición de dos conos idénticos: el del pozo real si no existiera la barrera y el del pozo imagen. Este pozo imagen suponemos que es un reflejo exacto del real: comienza a bombearen el mismo instante y el mismo caudal que el pozo real (y, por supuesto, que bombea en el mismo acuífero, que hemos supuesto indefinido).

En el caso real de un borde positivo el cono llegará a estabilizarse cuando todo el caudal extraído sea tomado por el acuífero del río o lago, quedando un cono asimétrico, como se aprecia en la figura. De nuevo podemos generar este resultado mediante la Teoría de las Imágenes: suponemos que el borde positivo no existe (el acuífero es ilimitado) y que al otro lado (de nuevo el borde actúa como un espejo) hay otro sondeo idéntico al real, pero que inyecta un caudal idéntico al que se bombea en el pozo real. El pozo imagen generaría un cono de ascensos idéntico al cono generado por el pozo real (si el acuífero fuera ilimitado) pero invertido. Cuando aplicamos el Principio de Superposición, ambos conos se anulan justo en el plano de simetría, coincidiendo con la realidad: el cono real al tocar el lago ya no baja más.

C.-Cálculo del descenso en un punto cualquiera (borde positivo o negativo):

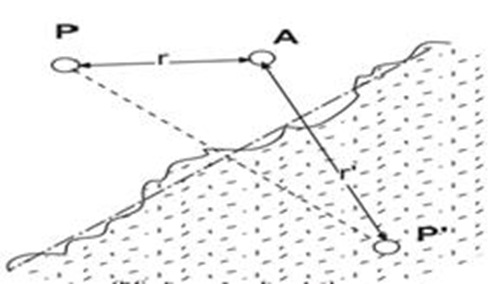
Como el pozo imagen no aparece en los mapas (¡!), si queremos aplicar esta teoría para conocer el descenso en un punto A cualquiera los pasos serán los siguientes:

1º. Asimilar el borde real, que siempre es irregular, a una recta

2º. Dibujar la perpendicular y el pozo imagen, simétrico de

P, utilizando la recta trazada en el punto anterior como plano de simetría.

3º. Medir, aplicando la escala del mapa, las distancias desde

A hasta los pozos real (P) e imagen (P’): r y r’

4º. Aplicar la fórmula correspondiente al tipo de acuífero para calcular el descenso producido en A por P (con la distancia r) y el producido en A por P’ (con la distancia r’), y sumar los resultados de ambos cálculos. Si es un borde positivo, el descenso en A debido a P’ será negativo: un ascenso.

C.1.-Cálculo del descenso estabilizado con un borde positivo (acuífero confinado, simplificación de Jacob):

En el caso de un borde positivo, se alcanzará el régimen permanente cuando toda el agua extraída por el pozo provenga del lago. Para acuífero confinado, podemos obtener la fórmula que nos proporcionará el descenso estabilizado. Utilizamos la última figura, suponiendo que el borde representado en ella es positivo:

Descenso en A producido por P:

Descenso en A producido por P’:

Recordemos que el caudal de P’ es el mismo que el de P, pero con diferente signo: QP’= -QP

Sumando los dos descensos se obtiene:

Hemos obtenido una fórmula de régimen permanente: no aparece el tiempo (t) ni el coeficiente de almacenamiento (S); nos proporciona el descenso estabilizado en función de la distancia al pozo real y al pozo imagen.

C.2.-Cálculo del descenso con un borde negativo (acuífero confinado, simplificación de Jacob):

En el caso de un borde negativo, el cálculo es similar, sumar los efectos producidos por el pozo real y el pozo imagen

Descenso en A producido por P:

Descenso en A producido por P’:

Como el caudal de P’ es el mismo que el de P, sumando los dos descensos se obtiene:

Se obtiene una fórmula casi idéntica a la original de Jacob, con dos diferencias: en el denominador, en lugar de r₂ aparece r. r’, y además aparece un 2: eso indica que el descenso producido será del orden del doble que si el acuífero fuera infinito. Eso tiene lógica ya que al pozo P no le llega agua por uno de sus lados (el borde impermeable). El descenso sería exactamente el doble que en acuífero infinito si el punto de observación considerado (A en la figura) estuviera justamente en el borde negativo, a la misma distancia de P que de P’ (en la fórmula se cumpliría que r. r’= r2).

Caudal específico y eficiencia

Concepto De Caudal Específico Y Eficiencia De Un Pozo

Se llama caudal especifico de un pozo al cociente entre el caudal de agua bombeando y el descenso dl nivel producido.

Siendo el descenso medido en el pozo.

El caudal específico de un pozo no es constante para un determinado caudal ya que con el tiempo el descenso aumenta. Sin embargo los descensos tienden a estabilizarse y por lo tanto el caudal especifico también.

Las curvas caudal-descenso y las curvas caudal especifico –descenso se llaman curvas características de un pozo.

El nivel de agua dentro de un pozo real es menor o a lo más igual al nivel de agua en el exterior del pozo puesto que existe una pérdida de carga al atravesar el agua la zona filtrante, contando como tal al macizo de gravas, si existe. El descenso adicional debido al paso por la zona filtrante se llama pérdida de penetración en el pozo.

De acuerdo con las consideraciones que se expondrán en los capítulos siguientes, es posible calcular el descenso teórico en el pozo. Se llama eficiencia del pozo a:

En la eficiencia del pozo intervienen las pérdidas de penetración en el pozo más las perdidas por circulación en la porción de acuífero próximo y dentro del propio pozo. Generalmente las primeras son las más importantes y de ahí la necesidad de seleccionar muy bien las zonas filtrantes.

Los pozos poco eficientes no son económicos por cuanto para bombear el mismo caudal que un pozo eficiente se precisan mayores descensos de nivel y por lo tanto mayor altura de bombeo, o si se tiene limitado el descenso, el caudal obtenido es menor.

La eficiencia de un pozo puede modificarse con el tiempo a consecuencia de varios fenómenos tales como aparición de incrustaciones, corrosión, sedimentación de arena en el pozo, etc. Las curvas características de un pozo relacionan el caudal extraído con el descenso en la captación al cabo de un cierto tiempo de bombeo y son de gran valor para apreciar la eficiencia de un pozo y sus variaciones.

En cierta forma un pozo incompleto contiene una causa de ineficiencia ya que en igual de condiciones se caudal especifico es menor que el de un pozo completo debido al incurvamiento de las líneas de corriente con aparición del efecto de anisotropía, y a la menor superficie de paso del agua. Es fácil deducir que los pozos abiertos solamente por el fondo son muy ineficientes bajo este ´punto de vista.

Todos estos conceptos expuestos son validos también para captaciones horizontales.