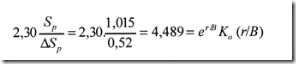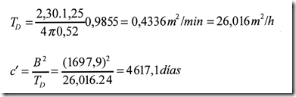· Campos de bombeo
Si en un acuífero se establecen varias captaciones de agua, éstas se influyen unas a otras ya que el descenso en cualquier punto de un acuífero es la suma de descensos provocados en él mismo por cada uno de los pozos considerados individualmente. El efecto de la presencia de varios pozos en un acuífero se traduce, pues, en que en cualquier pozo, para extraer un determinado caudal, es preciso elevar el agua a mayor altura que si estuviese solo. Esto crea un consumo adicional de energía de modo que realmente el establecimiento de un nuevo pozo en un campo de bombeo perjudica económicamente a los otros pozos existentes. En un acuífero libre se redice además el espesor saturado y por lo tanto la transmisividad, esto produce un nuevo incremento de descensos a una disminución de caudales si los descensos no pueden ser aumentados. No obstante, estas afecciones son necesarias si se quiere utilizar apropiadamente los recursos y capacidad de regulación de agua del acuífero en cuestión.
· Efectos de los límites de los acuíferos
Si el cono de descenso de un pozo alcanza un borde (las palabras borde y limite se manejaran como sinónimos al igual que la palabra barrera.) impermeable del acuífero, no puede extenderse en esa dirección y por lo tanto los descensos entre el pozo y los bordes han de ser mayores y más rápidos para poder proporcionar el agua que de otro modo hubiese sido suministrada por la extensión del cono más allá del borde en cuestión. Si el borde no es del todo impermeable (por ejemplo disminución lateral de la permeabilidad del acuífero) el efecto es algo más amortiguado y el cono puede extenderse algo más allá del borde.
De forma similar, sí el cono de descensos de un pozo alcanza un borde capaz de mantener el nivel contante, por ejemplo un río, un lago o el mar, el cono tampoco puede rebasar ese borde, pero ahora el agua precisa para el bombeo es suministrada por el citado borde y los descenso se estabilizan rápidamente.
Si el límite de potencial constante no es capaz de suministrar toda el agua necesaria (río con el lecho colmatado de limos, existencia de capas poco permeables que dificultan la infiltración, etc.) los niveles no se estabilizan y el cono rebasa el borde, pero los descenso se producen ahora más lentamente. Un efecto similar es producido por un aumento de la transmisividad del acuífero.
En un mismo campo de bombeo pueden coincidir varios timó de bordes o barreras (se llaman barreras negativas a los bordes impermeables y barreras positivas a los de potencial constante) y entonces el efecto que se tiene es la combinación de efectos a medid que el cono de descensos vaya alcanzando a los distintos limites.
El efecto de forzar la infiltración de agua superficial o de otros acuíferos por bombeo por bombeo en acuíferos directamente relacionados con ellos es llamado recarga inducida. El agua del río o lago para llegar al pozo debe sufrir un recorrido más o menos largo por el acuífero, con el consiguiente efecto de infiltrado y a veces de homogeneización, lo cual presenta un indudable interés practico.
· Ensayos de bombeo y puntos de observación
Un ensayo de bombeo es un ensayo realizado en condiciones predeterminas y controladas cuyo objetivo puede ser:
a) Establecer las características del acuífero,
b) Conocer el funcionamiento,
c) Determinar la correcta construcción del pozo.
El conocimiento de las características de un acuífero es importante en la programación de su óptimo aprovechamiento y es requisito necesario de cualquier investigación hidrogeológica. También tiene interés por cuanto permite predecir de forma razonable cuales va a ser los descensos y los caudales obtenibles de un pozo tanto a corto como a largo plazo.
Conociendo las características de un acuífero puede determinarse el descenso teórico en el pozo y por lo tanto valorar la eficiencia.
Los ensayos en el pozo, como único elemento de observación, permite valorar su eficiencia, trazar su curva característica también obtener algunas de las características del acuífero. Sin embargo, para lograr una aceptable precisión en los datos y valorar suficientemente el acuífero conviene realizar observaciones en otros puntos ya sean otros pozos o bien piezómetros especialmente instalados para ello. El ensayo observando únicamente el pozo de bombeo se llama a veces simplemente aforo.
La forma más común de realizar ensayos de bombeo es extrayendo agua a caudal constante y a partir de un instante en que se puede suponer que el nivel piezométrico del acuífero estaba estacionario. Los ensayos que miden en ascenso de niveles en un acuífero que previamente han sido bombeados durante un periodo conocido a caudal contante (ensayo de recuperación) son un importante complemento al ensayo de bombeo. También pueden realizarse ensayos de bombeo a descenso contante en el pozo, pero son raramente plateados. Sin embargo, pueden tener interés en el caso de disponerse de un pozo surgente en el que el descenso viene regulado por la posición de la boca de la perforación.
La observación de los descensos en un campo de bombeo se hace en pozos ya existentes o en perforaciones practicadas con ese fin. Si una tal perforación esta revertida con un tubo y ésta solo está abierta por el fondo ranurado en una longitud pequeña tenemos un piezómetro que se puede llamar puntal o perfecto, ya que mide el potencial hidráulico en el punto en el punto de abertura. En un mismo lugar y aún en el mismo acuífero, piezómetros abiertos a diferente profundidad pueden mostrar niveles diferentes. Si la longitud ranurada del piezómetro es importante en relación con el espesor del acuífero o con la distancia al pozo de bombeo, el nivel que se observa en el es un valor medio a lo largo de su parte activa entonces se trata de un piezómetro imperfecto, aunque no por ello deja de tener utilidad.
Los pozos de observación son muy frecuentemente piezómetros imperfectos.
Cuando la zona ranurada abarca todo el espesor del acuífero, se puede conocer el potencial medio, lo cual es de gran interés en muchos tipos de problemas.
Preparación ejecución ensayos de bombeo de pozos ensayos de inyección y recuperación – métodos
1.-PREPARACION Y EJECUCION DE LOS ENSAYOS DE BOMBEO
Al enfocar la solución de problemas de Hidrología Subterránea en pequeña o gran -escala, nos encontramos contínuamente ante la situación de poder obtener valores confiables y representativos de las características hidráulicas de los acuíferos. Los ensayos o pruebas de bombeo han probado ser el medio más adecuado para alcanzar ese objetivo.(3)
Como era lógico esperar, las pruebas de bombeo han sido interpretadas hasta muy recientemente partiendo del criterio de que el flujo es lineal en todo el campo alrededor del pozo. Sin embargo, como se sabe, tanto en acuíferos de baja como de alta conductividad hidráulica puede producirse flujo no lineal, lo que implica la necesidad de interpretar los ensayos con el criterio más general no lineal, que incluye como caso particular el lineal o Darciano. Además está claro que el único medio disponible para poder obtener los valores de los tres parámetros hidrogeológicos que caracterizan hasta el momento los acuíferos (k, C y E o sus propiedades asociadas) es la utilización del enfoque no lineal. Es utilizando ese nuevo enfoque que se presentarán la ejecución e interpretación de los distintos tipos de ensayos de bombeo.
2.- OBJETIVOS Y TIPOS DE PRUEBAS DE BOMBEO
La ejecución de las pruebas de bombeo responde en general a uno de los dos objetivos siguientes:
a) Estimar la cantidad de agua que puede extraerse de un pozo bajo condiciones previamente establecidas, o sea, con propósitos de aforo. En este tipo de pruebas, basta generalmente obtener información del pozo de bombeo y de dos pozos de observación o satélites.
b) Determinar las propiedades hidráulicas de un acuífero, para poder predecir posteriormente su comportamiento bajo situaciones diversas, evaluar la disponibilidad de recursos de agua subterránea, etcétera. En general, en este caso, es necesario obtener información de varios puntos seleccionados del acuífero, para lo cual se utilizarán varios pozos de bombeo con dos o más satélites cada uno. En la literatura rusa se denomina a este tipo de pruebas, aforos experimentales.
Por otra parte, desde el punto de vista del caudal extraído, las pruebas de pozo pueden realizarse a caudal constante o con abatimiento escalonado.
En las pruebas a caudal constante, éste debe mantenerse fijo durante toda la realización de la prueba, por lo que habrá necesidad de ir ajustándolo según pase el tiempo.
Se denominan pruebas de pozo con abatimiento escalonado a aquellas en que el caudal extraído del pozo se mantiene constante durante un tiempo, para cambiar súbitamente a otro caudal que se mantendrá constante durante otro tiempo, para volver a cambiar a un tercer caudal durante un tercer espacio de tiempo, y así sucesivamente.
El número de escalones (de caudales diferentes) deberá ser como mínimo tres, y los espacios de tiempo entre los cambios de caudal no tienen que ser iguales, aunque sí es recomendable que duren lo suficiente para que pueda utilizarse la aproximación de Jacob de la ecuación de Theis para flujo impermanente.
Las pruebas con abatimiento escalonado tienen la ventaja de poder determinar con ellas todas las propiedades hidrogeológicas de un mismo punto del acuífero sin necesidad de utilizar otra información que no sea la de ese punto, por lo que los resultados no quedarán afectados por las variaciones espaciales de las propiedades, sobre todo en el caso de los acuíferos con fracturas, fisuras o canales de disolución, que presentan gran heterogeneidad.
Aunque se han desarrollado métodos de análisis a base de abatimiento constante y caudal variable (6), un tipo de prueba basado en este criterio sería imposible de utilizar en la práctica, por las variaciones continuas que deben introducirse en el caudal, para mantener constante el abatimiento.
También se pueden determinar las propiedades hidráulicas de los acuíferos a través de pruebas de recarga, pero ese tipo de pruebas no será analizado ya que su utilización es poco frecuente.
Independientemente del propósito o del tipo de ensayo de bombeo que vaya a realizarse, se pueden distinguir claramente en ellos tres fases: el diseño de la prueba, la realización de las observaciones de campo y la interpretación de los resultados.
3.- DISEÑO DE LA PRUEBA DE UN ACUIFERO
Este es probablemente el más importante y más descuidado de los aspectos fundamentales de una prueba de bombeo.
El costo de una prueba de bombeo puede ser muy variable en dependencia de los objetivos que con ella se persiguen, pero en cualquier caso, resulta imprescindible diseñar adecuadamente el experimento para mejorar la probabilidad de que se obtengan los resultados esperados y evitar un malgasto de recursos.
El diseño previo de las pruebas, que vayan a ejecutarse en un acuífero tiene el propósito fundamental de obtener con una precisión aceptable, los valores de las características hidráulicas del medio. Para ello deberá evaluarse el lugar de la prueba, conocer previamente determinadas características del acuífero y tomar determinadas precauciones en relación con los pozos de bombeo, principales o de control y con los pozos de observación o satélites.(1,5)
4.-Evaluación del lugar de la prueba
La evaluación de las distintas facilidades existentes en el área donde nos proponemos realizar las pruebas es el primer paso a dar para preparar el diseño.
Debe hacerse un inventario de los pozos existentes tanto abandonados como bajo explotación, ya que la utilización de algunos de ellos puede significar una disminución del costo de la prueba, aunque pocas veces ocurre que la configuración, estado y distribución de los pozos existentes resulte adecuada para la ejecución de una prueba. El análisis de las facilidades existentes debe realizarse teniendo en cuenta las características que deben reunir los pozos de control y los de observación según aparece a continuación:
El pozo de control, de bombeo o principal
1. El pozo principal debe tener instalado un equipo de bombeo confiable, de capacidad adecuada para la prueba y con su equipo de control de caudal correspondiente.
2. Debe evitarse que el agua extraída pueda retornar al acuífero durante la prueba, por lo que debe ser conducida lejos del pozo de bombeo. Este aspecto es de importancia capital cuando se trata de un acuífero libre cuya superficie freática esté cercana a la del terreno.
3. Los dispositivos de descarga de la bomba deben permitir la instalación fácil de equipos para control remoto y regulación del caudal.
4. Debe ser posible medir adecuadamente el nivel del agua en el pozo de control, antes, durante y después de la prueba.
5. El diámetro, la profundidad total y la posición relativa de todas las aberturas de la camisa en el pozo de control deben conocerse detalladamente, es decir, todas las características del pozo.
Los pozos de observación o satélites
1. Se recomienda normalmente que los pozos satélite se dispongan en líneas que forman una cruz cuyo centro es el pozo principal. Cuando exista flujo natural en un acuífero, uno de los brazos de la cruz deberá estar orientado según la dirección del flujo y el otro normal a dicha dirección. (2) Cuando no sea posible económicamente perforar las 2 líneas de pozos, es conveniente que los pozos de observación se dispongan en la línea normal al flujo (1), en la cual el nivel estático de todos los satélites va a ser el mismo.
2. Los pozos de observación deben ser por lo menos 2 y estarán situados a distancias radiales del centro del pozo principal de 5 m y de 20 m. Cuando se puedan perforar mayor número de pozos estos deben situarse a 40 m, 80m y 10m del centro del pozo principal. Cuando por causas económicas en una prueba de aforo sólo se pueda perforar un pozo de observación, éste deberá situarse a 4 o 5m del pozo de control. Desde luego, que de esta forma habrá que utilizar el pozo principal para los cálculos de las propiedades hidráulicas, con los inconvenientes que de ello se deriven.
3. La respuesta de todos los pozos de observación a los cambios de nivel del agua debe probarse inyectando un volumen conocido de agua en cada pozo y medir inmediatamente la declinación del nivel del agua. El aumento inicial del nivel del agua debe desaparecer en no más de 3h, aunque resulta preferible una respuesta más rápida.
4. Deben conocerse la profundidad, el diámetro y los intervalos con rejilla de cada pozo de observación.
5. La distancia radial desde cada pozo de observación al centro del pozo de bombeo debe determinarse con la precisión necesaria, así como la posición de todos ellos en el plano.
5.- Información sobre el acuífero
Debe estar disponible o investigarse convenientemente la siguiente información sobre el acuífero.
1. Profundidad hasta el acuífero, espesor del mismo, así como los cambios en su configuración en el área que va a ser sometida a la prueba.
2. Planos o mapas de las discontinuidades del acuífero causadas por cambios en la litología o por la presencia de ríos y lagos.
3. Estimados de todas las propiedades hidráulicas pertinentes del acuífero y de las rocas adyacentes realizados por los medios disponibles. Si se sospecha la presencia de capas semiconfinantes ésto debe tenerse en cuenta al analizar los resultados de las pruebas.
6.-Importancia y objetivos de la evaluación previa a la prueba
La realización de una evaluación previa del lugar donde se ejecutará una prueba de un acuífero es muy importante. Es imprescindible tener en cuenta lo que hemos dicho respecto al pozo principal y los satélites, tanto para los pozos existentes como para los que se perforen con el propósito de ejecutar la prueba.
La evaluación previa del lugar de la prueba tiene propósitos principales:
a) Describir el acuífero, el pozo de control y los pozos de observación con el detalle suficiente, que permitirá enfocar correctamente su análisis.
b) Suministrar una base firme para predecir el valor relativo de los resultados de las pruebas teniendo en cuenta las facilidades existentes y llamar la atención sobre las posibles deficiencias en la localización de los pozos de observación y en otros aspectos.
Si la evaluación previa del lugar, indica que éste tiene características que se desvían notablemente de las que se suponen al deducir las fórmulas de pozo existentes, el lugar debe descartarse como zona de prueba.
Cuando las condiciones del lugar son complejas, como en el caso de acuíferos libres o pozos de penetración parcial, es obvio que resulta más difícil predecir los resultados de la prueba. No obstante, la predicción de los resultados debe realizarse en todos los sitios que se escojan para pruebas, ya que de ese modo podremos estar advertidos en contra de las deficiencias importantes, por ejemplo, en la configuración de la situación de los pozos y tomar una decisión acertada respecto a la perforación de uno o más pozos en puntos claves dentro del sistema.
Los acuíferos confinados son más fáciles de someter a pruebas que los libres, a causa de que tienen condiciones de contorno más simples. En los sistemas no confinados la movilidad del contorno superior (superficie freática), las componentes verticales del flujo y la entrega no lineal del agua desde el almacenaje, son problemas difíciles de tratar, aunque, sin embargo, estos problemas han podido analizarse con éxito recientemente. Debemos recordar, además, que el flujo libre se puede tratar como confinado dentro de ciertos límites.
En la época anterior a que se hubieran podido estudiar analíticamente los efectos del flujo vertical y la entrega retardada de los acuíferos libres, la práctica común era bombear un "tiempo suficiente" de tal modo que esos efectos se conviertan en despreciables y se pudiera aplicar el modelo más simple del flujo artesiano. Sin embargo no había un verdadero criterio que cuantificara ese "tiempo suficiente". En la actualidad, las soluciones analíticas existentes han permitido elaborar algunos criterios para definir el "tiempo suficiente" para poder obtener una respuesta artesiana de un acuífero libre.
En la referencia se mencionan varios de esos criterios, entre ellos el elaborado por Boulton y por Hantush, que expresa que las componentes verticales del flujo afectan significativamente la respuesta del acuífero, para tiempos:
t < 5 m E/Kz
en la región
0 r/m < 0,2
donde Kz: es la conductividad hidráulica lineal vertical del acuífero y los demás símbolos, tal como han sido definidos anteriormente.
7.- REALIZACION DE LA PRUEBA. OBSERVACIONES DE CAMPO
En general, las pruebas de pozo se ejecutan a caudal constante o con abatimiento escalonado.
Las pruebas a caudal constante deben hacerse con 2 caudales diferentes por lo menos, que estén entre sí en una relación mínima de 2 a 3. Las pruebas con abatimiento escalonado deben hacerse con 3 caudales diferentes por lo menos, con relaciones entre 2 caudales sucesivos de 2 a 3 ó 1 a 2. En todos los casos, el caudal mayor utilizado, será ligeramente superior al que se propone para la explotación.
En cualquier caso resulta necesario en toda prueba tener determinada información sobre las características de los pozos y los records de la variación de los niveles y del caudal extraído. Todo esto constituye lo que se conoce como observaciones del campo.
Los records que se necesitan para el análisis y las tolerancias que se consideran generalmente aceptables en las mediciones (1), son las siguientes:
1. Caudal del pozo de control: ![]() 10%
10%
2. Profundidad hasta el agua en los pozos, por debajo del punto de referencia: ![]() 3mm
3mm
3. Distancia del pozo de control a cada pozo de observación: ![]() 0,5%
0,5%
4. Descripción de los puntos de referencia
5. Elevación de los puntos de referencia: ![]() 3mm
3mm
6. Distancia vertical entre los puntos de referencia y la superficie del terreno: ![]() 30mm
30mm
7. Profundidad total de los pozos: ![]() 1%
1%
8. Profundidad y longitud de los intervalos con rejillas en todos los pozos: ![]() 1%
1%
9. Diámetro, tipo de camisa, tipo de rejilla, método de construcción de todos los pozos.
10. Localización de todos los pozos en planta en relación con algún levantamiento topográfico o por coordenadas de latitud y longitud (la precisión dependerá de lo que necesitemos en cada caso), pero sobre todo debe estar bien clara la posición de los pozos de observación respecto a los de control.
La litología y las características de construcción de los pozos de observación y el de control se obtendrán, según el caso, entrevistando al responsable del lugar o al que los perforó o de los records litológicos y de las características constructivas que deben prepararse cuando el pozo haya sido construído específicamente para la prueba.
8.-Observación de los niveles del agua
Las fórmulas de flujo hacia los pozos se basan, generalmente, en el cambio de la carga, h, o en el cambio de abatimiento S. Es muy importante recordar que los cambios de profundidad hasta el agua, observados durante la prueba pueden incluir componentes debidas a otras variables, como son, por ejemplo, las variaciones de la presión atmosférica, el efecto de las mareas y una posible recarga del acuífero. Por otra parte, el flujo natural en la mayoría de los acuíferos es generalmente diferente de día a día, por consiguiente se hace necesario observar las profundidades hasta el agua durante un tiempo anterior a la prueba, para determinar la tendencia del nivel del agua y usarla al calcular los abatimientos (Fig. 2.1).
Fig.2.1 Hidrograma de un pozo de observación indicando el abatimiento sobre la base de la tendencia del nivel del agua subterránea cuando no existe extracción.
La observación de los abatimientos con precisión sólo puede lograrse con una buena predicción de la tendencia del nivel del agua o si los efectos de abatimiento de la prueba son grandes en relación con otros efectos.
El período de observación anterior al comienzo de la prueba (anterior a t=0), deberá ser, como regla general, al menos del doble del tiempo que dure la prueba de bombeo.
En las zonas de prueba correspondientes a acuíferos artesianos debe llevarse un récord contínuo de la presión atmosférica (con sensibilidad de 3mm de mercurio) durante los períodos de prueba y de identificación de la tendencia del nivel anterior a la prueba. Este récord permitirá realizar los ajustes pertinentes.
A partir de las mediciones del nivel del agua antes de comenzar la prueba, de igual modo que se identifican los efectos de la presión atmosférica, podrán identificarse otras perturbaciones del nivel del agua tales como las que producen la operación de pozos cercanos, la recarga del acuífero y las sobrecargas producidas por trenes o fenómenos sísmicos.
Durante la prueba, la profundidad hasta el agua en cada pozo, debe medirse con frecuencia suficiente para que podamos contar con un buen número de observaciones en cada ciclo logarítmico (alrededor de 8 a 10, por ejemplo). Esto puede lograrse, por ejemplo, si ejecutamos mediciones del nivel en los tiempos t=1, 1 1/2, 2, 3, 4, 5, 6, 8 y 10 min y en todos los múltiplos de 10 de esos tiempos en los ciclos siguientes.
Durante las 2 h ó 3 h primeras a partir de que se inicia la prueba es preferible que haya un observador en cada uno de los pozos de observación y en el de control. Despúes de los 300 minutos las mediciones se harán con espacios de tiempo de 100minutos o más entre sí; en ese caso, podrá utilizarse un solo observador para tomar toda la información, ya que le resultará relativamente fácil trasladarse a los distintos lugares en un tiempo relativamente corto; eso sí, las mediciones deberá hacerlas siempre siguiendo una misma secuencia.
Aunque no es totalmente imprescindible medir todos los pozos simultáneamente, sí es conveniente conseguir una separación uniforme de los abatimientos en la escala logarítmica del tiempo. El tiempo anotado para cada observación debe ser el real. Todos los cronómetros utilizados deben sincronizarse antes de iniciar las pruebas y deben tomarse las precauciones necesarias para que cada observador sea notificado en el instante en que comenzó la prueba.
Como ya hemos visto anteriormente, en el pozo de bombeo es necesario tener en cuenta las pérdidas que pueden ocurrir aparte de la correspondiente a la resistencia del acuífero, por eso es imprescindible tener toda la información relativa a las características de construcción de dicho pozo.
Durante la realización de la prueba deben anotarse todos los detalles que permitan posteriormente identificar cualquier aberración en las observaciones de los niveles. Cuando se quiera utilizar el método de recuperación, deberá medirse el nivel del agua a partir de que cese el bombeo, haciendo también 8 a 10 mediciones por ciclo logarítmico.
9..-Medición del caudal
El caudal obtenido en el pozo principal se mide normalmente haciendo pasar el flujo por una restricción, para la cual se conoce la curva de calibración. En los manuales de hidráulica hay abundancia de descripciones y calibraciones de este tipo de dispositivos. En caso de no poder contarse con dispositivos semejantes, puede utilizarse un recipiente previamente tarado en el que se medirá el tiempo de llenado del mismo.
En las pruebas a caudal constante es importante medirlo periódicamente y ajustarlo en caso necesario. La frecuencia de medición y ajuste del caudal durante una prueba depende de la bomba, el pozo, el acuífero y las características de la energía disponible. No obstante, es recomendable que durante la primera hora de bombeo el caudal se mida por lo menos 3 veces, y se ajuste en caso necesario, ya que en ese espacio de tiempo es cuando más rápidamente crece el abatimiento y por consiguiente la carga de bombeo.
A partir de la primera hora de bombeo, deberá medirse y ajustarse con intervalos de 100 minutos a 200 minutos coincidiendo con alguno de los momentos en que se realicen observaciones del nivel. En todos los casos se tendrán los cuidados necesarios para mantener el caudal dentro del rango deseado, y no debe permitirse que varíe por encima de -- 10%, ya que mayores variaciones producirían aberraciones en los abatimientos que son muy difíciles de tratar en el momento en que vayan a analizarse los datos tomados durante la prueba.
Debe tomarse nota de cualquier cosa que pueda resultar de interés posteriormente, cuando los datos de la prueba vayan a ser analizados. Cuando la prueba requiera cambios en el caudal, como en las pruebas con abatimiento escalonado, la descarga de la bomba debe poder regularse por una válvula de cuña para ajustarse rápida y fácilmente a los distintos caudales programados.
LOS ENSAYOS DE BOMBEO
Una vez alcanzado el acuífero mediante un sondeo o pozo hay que verificar de forma práctica sus características. No basta saber que hay agua. Hace falta conocer cuánta hay. Qué caudal (litros por segundo) podemos extraer.
Los “ensayos de bombeo” sirven para este fin. Se extrae durante cierto tiempo, dos días por ejemplo, un caudal del acuífero a través del pozo. Se controla como varía el nivel del agua en el pozo a lo largo de este tiempo.
En general, si baja poco, el acuífero puede ser bueno. Puede suministrar ese caudal con ese sondeo. Las características del acuífero (permeabilidad, coeficiente de almacenamiento, espesor, etc.) son idóneos.
A veces puede ocurrir que por mala ejecución del sondeo o pozo de captación
el resultado del ensayo sea negativo. A pesar de que el acuífero en sí tenga buenas características. Esto ocurre, por ejemplo, cuando no se disponen
adecuadamente los filtros entre la pared del terreno y la tubería. Si la obra está mal hecha, se “atoran”. Su resistencia al paso del agua aumenta.
En la experiencia del ensayo de bombeo habrá que tener cuidado para que las aguas extraídas no nos confundan. Habrá que verterlas lejos. O en algún punto,
tal que aunque se filtren, no vuelvan a engrosar el nivel en el lugar en que se realiza el bombeo.
Para conocer aún mejor las características del acuífero, se realizan a veces otros controles. Se inyectan en el terreno o en sondeos, pequeñas cantidades
de un producto fácilmente distinguible, que se disuelve en el agua. Después sale por fuentes naturales o por otros pozos y sondeos. Así puede saberse
cómo se mueven las aguas subterráneas.
1.- LA ESTRUCTURA DE UN POZO DE BOMBEO
El pozo de bombeo, perforado en un acuífero por cualquier procedimiento, podrá estar provisto de una estructura, cuando sea necesaria para garantizar la estabilidad de las paredes de la perforación. Esta estructura ocupará una parte del espacio interior definido por la cara del pozo (figura 1.3)
En su forma más general, tal como aparece representada en la figura 1.3, la estructura del pozo, al atravesar el acuífero, puede estar compuesta por un empaque de grava y una camisa, total o parcialmente convertida en rejilla, que permitirá que el agua entre a dicha camisa para ser extraida por la bomba:
Fig. 1.3 Representación esquemática de la estructura de un pozo de bombeo y de las zonas características en su cercanía.
Las operaciones de perforación y el desarrollo del pozo afectarán al acuífero más allá de la cara del pozo. El desarrollo remueve el material más fino del acuífero, corrigiendo cualquier afectación o colmatación en la formación geológica originadas como efecto colateral del proceso de perforación. Asimismo, estabiliza la formación alrededor del pozo, de modo que el agua extraída estará desprovista de arena y aumenta además la porosidad y la permeabilidad de la formación natural en la vecindad del pozo de extracción. (2)
Es decir, que en la práctica, una vez desarrollado el pozo, se formará una zona de desarenado más permeable que el acuífero, que se extenderá desde la cara del pozo hasta una distancia rda, que definirá el comienzo de la formación acuífera no alterada. (2)
De esa forma, quedan definidas tres zonas alrededor de la camisa del pozo:
- Zona del empaque de gravas, comprendida entre las distancias radiales rw y rp.
- Zona de desarenado, comprendida entre las distancias radiales rp y rda.
- Zona del acuífero no alterado, situada más allá de la distancia radial rda.
Las distancias radiales que definen estas zonas, están definidas como:
rw, distancia del centro del pozo a la cara interior de la tubería de revestimiento (camisa) y rejilla.
rp, distancia del centro del pozo hasta el límite exterior del empaque de grava (cara del pozo).
rda, distancia del centro del pozo hasta la formación acuífera no alterada.
Como cada zona tiene sus características hidrogeológicas propias, el abatimiento que se produce en el pozo, Sw, para el caso de un acuífero confinado, estará formado por varias componentes y podrá expresarse como (7).
donde:
Srda, abatimiento producido en el acuífero no alterado a la distancia rda
abatimiento adicional que se produce en la zona de desarenado (diferencia en abatimiento entre las distancias rp y rda)
abatimiento adicional que se produce en el empaque de gravas (diferencia en abatimiento entre las distancias rw y rp)
, pérdida de carga en la rejilla y la tubería de revestimiento del pozo (camisa)
A partir del análisis de estas componentes del abatimiento el autor ha podido formular una nueva ecuación característica para el pozo de bombeo (7), que aparece más adelante como ecuación 3.8.
2.-. ECUACIONES BASICAS PARA EL ANALISIS DE LOS ENSAYOS DE BOMBEO
Según el agua se mueve desde el radio de influencia hacia el centro de un pozo, aumentará el gradiente para poder aumentar la velocidad en proporción a la disminución del área cilíndrica a través de la cual fluye el agua. Este aumento de velocidad implica un aumento del número de Reynolds según se esté más cerca del pozo, lo que da lugar a la posibilidad de que aún cuando el régimen en las zonas más alejadas sea darciano, cambie a no lineal (se desvíe de la ley de Darcy) en una región más o menos cercana al pozo. Esto estará en función del caudal extraído y de las características hidrogeológicas del acuífero.
Es lógico que de existir desviaciones de la ley de Darcy, éstas se hagan más evidentes en el propio pozo o en la zona de acuífero inmediata a él.
Sin embargo, en general ha sido costumbre atribuir las desviaciones de la ley de Darcy observadas en los pozos a pérdidas de carga producidas por el paso del agua a través de su estructura (empaque de gravas, rejilla y camisa), considerándose que en el acuífero propiamente dicho, sólo ocurre flujo lineal o darciano.
Este punto de vista no es válido como criterio general ya que se ha comprobado que en la práctica, tanto en acuíferos de alta como baja conductividad hidráulica, en zonas más o menos alejadas del pozo de bombeo, se producen desviaciones importantes de la ley de Darcy y se presenta el flujo no lineal (6,10). O sea que el análisis del flujo hacia los pozos deberá hacerse siempre partiendo del enfoque no lineal.
Lo anterior implica que pueden aparecer alrededor del pozo de bombeo los distintos regímenes de circulación del agua subterránea (desde el darciano al turbulento puro), pero, ¿cómo determinar en forma sencilla las zonas en que ocurren los diferentes tipos de flujo y los límites que las separan? De acuerdo con lo propuesto por Pérez-Franco (8), si se tiene en cuenta que para un caudal determinado, Q, la velocidad aumenta según disminuye el área de flujo hacia el centro del pozo, la imagen más completa del flujo alrededor del mismo, debería concebirse como formada por un máximo de tres zonas, tal como aparece en la figura 3.1, que van de flujo turbulento puro en la zona más cercana al pozo, hasta flujo darciano en la zona más alejada, pasando por una intermedia de flujo no lineal. De acuerdo con las características del acuífero y el caudal extraído, en algunos casos existirá una sola zona: la lineal o darciana; en otros, dos zonas: la lineal y la no lineal, y en otros las tres zonas.
Fig.3.1 Zonas de flujo alrededor de un pozo
El límite entre las zonas de flujo no lineal y lineal, está definido por el llamado radio de Darcy, r D, que se expresa como (8):
El límite entre las zonas de flujo no lineal y turbulento puro, está definido por el llamado radio turbulento, rT, que se expresa como (8):
Por comparación entre las ecuaciones 3.1 y 3.2 resulta:
Comparando los valores de r D y r T con el del radio del pozo, rP, puede definirse fácilmente el número y tipos de zonas existentes y la imagen completa del flujo alrededor del pozo para el caudal correspondiente. De ese modo:
Si r D Si r D > r P y r T Si r T > r P existirán las tres zonas de flujo
Independientemente del número de zonas de flujo que puedan distinguirse alrededor del pozo, basta que r D sea mayor que r P para que haya que aplicar necesariamente el enfoque no lineal para analizar el flujo hacia el pozo. Por otra parte, si se utiliza el enfoque no lineal y el flujo es darciano en todo el campo, el propio proceso de cálculo lo indicará sin dar origen a ninguna dificultad en el análisis. Es por eso que se recomienda utilizar siempre el enfoque no lineal.
También se acostumbra hablar de métodos de equilibrio y métodos de no equilibrio (flujo impermanente). Realmente, si se hace un ensayo de bombeo, no cuesta ningún trabajo anotar las informaciones pertinentes que ocurren a través del tiempo y aprovechar las inmensas ventajas que se derivan de usar los métodos que se basan en flujo impermanente. Es por eso, que las ecuaciones que se presentan para analizar los distintos tipos de acuíferos solamente serán para flujo impermanente, que de hecho contienen en sí como casos particulares los que corresponden a flujo permanente (condiciones de equilibrio).
La duración de los ensayos para la mayoría de los propósitos no tiene que pasar de 8 a 10 horas y sólo deben prolongarse cuando se haga necesario discriminar la existencia de fronteras geológicas que limitan el acuífero, ya sean éstas positivas o negativas.
3.- REPRESENTACION GRAFICA DE LOS RESULTADOS DE LOS ENSAYOS DE BOMBEO
Para representar los resultados de los ensayos de bombeo ha sido costumbre utilizar tres tipos de gráficos:
a) gráficos de tiempo-abatimiento
b) gráficos de distancia-abatimiento
c) gráficos de tiempo-distancia-abatimiento
Estos gráficos se han utilizado normalmente para determinar las propiedades hidrogeológicas y otras características de los acuíferos, (1) sin embargo, la probabilidad de que ocurra flujo no lineal hacia el pozo de extracción limita las posibilidades de utilización de los mismos en relación con lo acostumbrado. (5)
La representación gráfica de los resultados de los ensayos puede hacerse en escala aritmética, logarítmica o semilogarítmica. Los gráficos en escala aritmética se utilizan poco y tienen escaso valor práctico. (4) Los gráficos en escala logarítmica son útiles para reconocer el tipo de acuífero (3) y para determinar las propiedades de los mismos. Los gráficos semilogarítmicos son los que más se utilizan y los que brindan en general una mayor potencialidad de análisis.
Los gráficos de tiempo-abatimiento representan la relación entre el abatimiento, Sr, en un punto del acuífero situado a una distancia r del centro del pozo de bombeo y el tiempo, t, a partir del comienzo del bombeo. Generalmente el tiempo se representa en el eje de las abscisas y el abatimiento en el eje de las ordenadas.
Los gráficos de distancia-abatimiento representan el abatimiento que se ha producido en un instante de tiempo, t, determinado a partir de que se inició el bombeo, a las distancias radiales a que se encuentran los distintos puntos del acuífero. O sea, que este tipo de gráfico describe la forma del cono de abatimiento o depresión para un instante determinado. Generalmente la distancia se representa en el eje de las abscisas y el abatimiento en el de las ordenadas.
Como se ha visto, la información que brinda el gráfico de tiempo-abatimiento es para un punto determinado del acuífero y la que brinda el de distancia-abatimiento es para un tiempo determinado. Para analizar en un solo gráfico los diferentes puntos del acuífero para los distintos tiempos, es costumbre utilizar gráficos que relacionan el abatimiento con la cantidad t/r2 (1, 4) y que el autor ha denominado gráficos de tiempo-distancia-abatimiento (5).
Se sabe que la ecuación general del flujo hacia un pozo en régimen impermanente no lineal está expresada para acuíferos libres y confinados, por:
lo que puede expresarse abreviadamente como:
donde: SD, componente lineal del abatimiento, expresada por el primer término del segundo miembro de la ecuación 3.4
ST, componente turbulenta del abatimiento, expresada por el segundo término del segundo miembro de la ecuación 3.4
Sobre la base de la representación gráfica de esta ecuación se hará a continuación el análisis de la utilización de los distintos tipos de gráficos y sus limitaciones.
4.- USO DE LOS GRAFICOS DE DISTANCIA-ABATIMIENTO
Los gráficos de distancia-abatimiento se presentan generalmente en dos formas:
a) en escala aritmética
b) en escala semilogarítmica
El gráfico en escala aritmética tiene poca utilidad y prácticamente no se usa.
Los gráficos en escala semilogarítmica relacionan Sr con log r. Para analizar la utilización de este tipo de gráficos hay que distinguir si el flujo hacia el pozo es lineal en todo el campo de flujo alrededor del mismo, (rp
Para el caso del flujo lineal, la ecuación general 3.4 queda reducida a la componente lineal del flujo, o sea que:
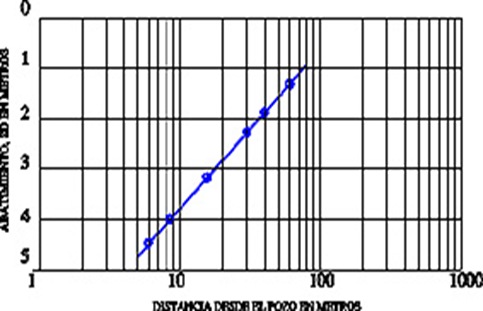
Para régimen lineal impermanente, los gráficos semilogarítmicos de distancia-abatimiento para un instante determinado se preparan en papel semilogarítmico, con el abatimiento en la ordenada en escala aritmética y la distancia en escala logarítmica en el eje de las abscisas, y son en realidad una representación gráfica en ese instante de la traza de la superficie del cono de depresión en un plano vertical, o sea, de la curva de abatimiento. En este caso, la curva de abatimiento estará representada por una recta, tal como muestra la figura 4.1.
Fig. 4.1 Representación de la curva de abatimiento en gráfico semilogarítmico
Porqué para flujo lineal la curva de abatimiento en escala semilogarítmica es una recta, puede reconocerse analizando la ecuación 4.2. De acuerdo con dicha ecuación, para un tiempo determinado, t = constante, la diferencia de abatimiento entre dos puntos situados a las distancias r1 y r2 del centro del pozo principal (el punto 2 es el más alejado) puede expresarse como:
Se ve claramente que la ecuación 4.4 representa una recta en el plano abatimiento-logarítmico de la distancia. En esta situación la intersección de la recta con el eje de las abscisas (SD = O), representa el radio de influencia (rO) para el instante considerado. Además se podrán determinar TD y E en condiciones de flujo lineal (4, 6). En forma general se recomienda que haya información al menos de tres puntos para poder trazar una buena recta de ajuste.
Sin embargo, en el caso del flujo no lineal, la representación no es una recta, sino una curva que quedará claramente definida por dichos tres puntos.
Si se analiza la ecuación 3.4 se puede observar que la componente turbulenta del abatimiento puede expresarse también como:
La representación de la ecuación general no lineal (ecuación 3.4) en el gráfico Sr vs log r para un tiempo fijo, se hará analizando sus componentes:
La componente lineal, SD, estará representada por una línea recta (E-F, figura 4,2), sin embargo, según revela la ecuación 4.5 la componente turbulenta es función del inverso de la distancia y no del logarítmico de la distancia, de donde resulta que la suma de las dos componentes, o sea, el abatimiento total, Sr, quedará representado por una curva (GHI, figura 4.2).
Fig. 4.2 Gráfico de distancia-abatimiento
De lo anterior resulta que el gráfico de distancia-abatimiento no puede utilizarse cuando el flujo es no lineal con los propósitos acostumbrados de determinar TD, E y ro.
Por otra parte, para conocer si el flujo que ocurre es lineal o no lineal haría falta tener tres pozos de observación situados a diferentes distancias, lo que permitiría reconocer si los tres puntos correspondientes al representarlos en el gráfico de distancia-abatimiento están en línea recta (flujo lineal) o no lo están (flujo no lineal). Como en la mayoría de los casos de lo que se dispone cuando más es de dos pozos de observación, no se tendría la seguridad de si se puede utilizar o no el gráfico de distancia-abatimiento para determinar las propiedades. Como por otra parte, el flujo no lineal puede presentarse en cualquier tipo de acuífero (7), es preferible no utilizar este tipo de gráfico en el análisis de los resultados de los ensayos de bombeo.
5.- TIPO DE GRAFICOS QUE ES PREFERIBLE UTILIZAR EN EL ANALISIS DE LOS ENSAYOS DE BOMBEO
Del análisis realizado sobre los distintos tipos de gráficos que ha sido costumbre utilizar en la interpretación de los ensayos de bombeo y las limitaciones que se presentan en algunos de ellos se pueden resumir las siguientes conclusiones:
a) Los gráficos de Sr-log (t/r2) no pueden utilizarse cuando el flujo es no lineal.
b) Cuando el flujo es no lineal, el gráfico semilogarítmico de distancia-abatimiento es una curva y no es posible utilizarlo con los propósitos acostumbrados.
c) Los gráficos semilogarítmicos de tiempo-abatimiento se pueden utilizar en régimen no lineal con los objetivos acostumbrados con la única advertencia de que hay que determinar el coeficiete de almacenamiento por un procedimiento diferente al usado corrientemente.
d) Como de los gráficos de tiempo-abatimiento se puede obtener toda la información que se podrá lograr de los otros tipos de gráficos y no están limitados en su uso cuando ocurre flujo no lineal, resulta recomendable basar el análisis gráfico de los resultados de los ensayos de bombeo solamente en procedimientos de tiempo-abatimiento.
6.- RECONOCIMIENTO DEL TIPO DE ACUIFERO A TRAVES DE LA REPRESENTACION GRAFICA DE LOS RESULTADOS DE LOS ENSAYOS DE BOMBEO
Como ya se ha dicho, la forma de los gráficos de tiempo-abatimiento en escala doble logarítmica, permite identificar el tipo de acuífero. En la figura 4.3 aparecen las curvas típicas de tiempo-abatimiento para acuíferos confinados, semiconfinados, semilibres o libres con entrega retardada y para acuíferos libres. De ese modo, disponiendo de gráficos logarítmicos los resultados de los ensayos de bombeo, y comparando la forma de la curva que los representa con las formas típicas de la figura 4.3 se podrá reconocer el tipo de acuífero y proceder al análisis de los resultados con las ecuaciones correspondientes.
A.- IDENTIFICACION DE FRONTERAS HIDROGEOLOGICAS A TRAVES DE LOS GRAFICOS DE TIEMPO-ABATIMIENTO
Como se ha dicho, para un acuífero confinado por ejemplo, la representación de los resultados de un ensayo de bombeo en un gráfico semilogarítmico de tiempo-abatimiento es una línea recta. Como se sabe, el abatimietno aumenta y el cono de depresión se expande a medida que pasa el tiempo. La tendencia del abatimieto queda definida por la línea recta del gráfico, pero si el cono de depresión en su avance alcanza una zona de recarga o una frontera impermeable, quedan modificadas las superposiciones sobre las cuales descansa la extensión indefinida de la línea recta (acuífero de extensión infinita y procedencia del agua extraída sólo del almacenamiento) y ese cambio aparecerá en el gráfico como un cambio de pendiente, a causa del consecuente aumento o disminución del abatimiento.
En el caso de recarga, el abatimiento disminuirá proporcionalmente a ésta y si es capaz de suministrar el caudal completo de bombeo, el abatimiento quedará estabilizado en el valor correspondiente al momento en que el radio de influencia del pozo en su avance hizo contacto con la recarga (ver figura 4.5).
Fig. 4.5 Intersección de la curva , con la zona de recarga
En el caso, por ejemplo, de una frontera impermeable, de modo semejante, cuando el creciente radio de influencia toque la frontera, el abatimiento aumentará a un ritmo superior al que venía aumentando anteriormente (ver figura 4.6)
Fig. 4.6 Intersección de la curva , con una frontera impermeable
La localización de la zona de recarga o de la frontera impermeable es muy sencilla. Como se sabe el radio de influencia en un instante determinado, t, está representado por:
Tomando del gráfico de tiempo-abatimiento el valor del tiempo correspondiente al punto en que cambia la pendiente de la recta que representa los resultados del ensayo de bombeo y calculando con ese tiempo, ro por la ecuación 4.9 se obtendrá la distancia a que se encuentra la zona de recarga o la frontera impermeable.
6. INTERPRETACION DE LOS RESULTADOS DE LOS ENSAYOS DE BOMBEO
El primer paso que debe seguirse al proceder a analizar los resultados de un ensayo de bombeo, es disponer la información del ensayo en un gráfico de tiempo-abatimiento en escala doble logarítmica lo que permitirá en muchos casos reconocer el tipo de acuífero. Una vez que se conoce el tipo de acuífero se procederá a determinar sus propiedades utilizando las ecuaciones correspondientes. En general, las propiedades podrán determinarse por procedimientos analíticos o procedimientos gráficos. En lo que sigue, se presenta para cada tipo de acuífero un método de análisis de los diversos que hay para cada caso.
6.1.- DETERMINACION DE LAS PROPIEDADES DE ACUIFEROS CONFINADOS Y LIBRES POR ENSAYOS A CAUDAL CONSTANTE
Procedimiento analítico
Con pruebas a caudal constante, para poder determinar todas las propiedades del acuífero, es necesario tener información al menos de dos pozos de observación situados a distancias diferentes del centro del pozo de bombeo (4). Uno de los procedimientos que puede seguirse (6) es la determinación de TD, TT y E en ese orden.
Para determinar TD se parte de la ecuación 3.4, aplicada a cada pozo de observación para dos tiempos diferentes tA y tB (tB >tA >50 min) o sea que, si se tienen dos pozos de observación resultará: para tA en el pozo de observación #1.
para tB en el pozo de observación #1
Haciendo el mismo análisis para el pozo de observación #2, resulta:
de modo que:
y también:
Es bueno aclarar que para el tiempo tB debe seleccionarse el mayor posible en que se tenga la seguridad de que el flujo hacia el pozo no ha llegado al equilibrio.
Los valores de TD para ambos pozos de observación se promedian, aunque si son muy diferentes, el resto de las propiedades que se calcularán tendrán una representatividad menor que si los valores obtenidos para TD son muy parecidos.
Una vez determinada TD, para calcular TT, se aplica la ecuación 3.4 a los datos de dos pozos de observación, para un mismo tiempo tc. Así se tendrá que:
Como el abatimiento en el pozo más cercano para un tiempo determinado es mayor que el abatimiento en el pozo más alejado para el mismo tiempo, restando la ecuación 5.7 de la 5.8 se obtiene:
En la ecuación 5.9 todos los datos son conocidos excepto TT. Luego, despejándola se puede calcular sin dificultad.
Para calcular E, conocidos TD y TT, se usa la ecuación 3.4 para un tiempo mayor que 50 minutos y lo mayor posible en cualquiera de los pozos de observación. Si se observa la ecuación 3.4, o sea:
se verá que en esta fase del proceso de análisis, si se le supone al radio de influencia un valor razonable, el único valor desconocido será el del coeficiente de almacenamiento, que podrá calcularse sin dificultad a partir de la ecuación 3.4. Una vez obtenido este valor aproximado de E, se calculará el valor del radio de influencia correspondiente al tiempo con que se calculó E, utilizando la ecuación 4.9, o sea:
Si el valor calculado para ro por esta ecuación coincide con el que se supuso para calcular inicialmente E, el valor obtenido para E será el correcto, si no coincide, se volverá a calcular E con el nuevo radio de influencia, iterando hasta que exista aproximación suficiente.
De ese modo quedan determinados los parámetros TD, TT y E, de los cuales pueden obtenerse KD y KT ó k y C, utilizando las ecuaciones de transformación correspondientes.
Procedimiento gráfico
Para determinar las propiedades de un acuífero confinado utilizando el procedimiento gráfico, se representan en un gráfico semilogarítmico de tiempo-abatimiento los resultados del ensayo de bombeo en cada pozo de observación tal como aparece en la figura 5.1 para dos de ellos:
Fig. 5.1 Gráfico semilogarítmico de los resultados de un ensayo de bombeo
Se trazarán las rectas de mejor ajuste para cada pozo y de su pendiente se determinará el valor de TD, teniendo en cuenta lo expresado por la ecuación 5.3 ó la 5.4 que la diferencia en abatimiento para dos tiempos diferentes en uno cualquiera de los pozos de observación es:
que expresada en logarítmos de base 10 se transforma en:
Si se designa por ![]() S la diferencia en abatimiento por ciclo logarítmico del tiempo, ocurrirá que para cada ciclo logarítmico tB = 10 tA, de modo que la ecuación 5.11 se transformará en:
S la diferencia en abatimiento por ciclo logarítmico del tiempo, ocurrirá que para cada ciclo logarítmico tB = 10 tA, de modo que la ecuación 5.11 se transformará en:
luego:
El valor de TD se calculará para cada recta que represente los resultados del ensayo en un pozo de observación y se promediará.
Para determinar TT se buscará en el gráfico, (figura 5.1) la diferencia media en abatimiento entre dos pozos de observación (Sr1-Sr2 ), que tal como lo expresa la ecuación 5.9 resulta:
de la cual puede calcularse TT, ya que es la única incógnita en esa ecuación.
Para calcular E, se calcula el valor de la componente turbulenta del abatimiento para el pozo de observación más cercano al pozo de bombeo, que de acuerdo con la ecuación 3.5 tiene el valor aproximado de:
y se resta de la recta que representa Sr-log t, con lo que quedará una recta que corresponderá al valor de la componente lineal del abatimiento para ese pozo de observación, o sea:
que expresada en logaritmos de base 10 resulta:
Si se extiende la recta que representa la componente lineal SD hasta cortar el eje del tiempo en toB, para ese tiempo SD = O y por consiguiente resultará que:
De donde resulta que:
ecuación que permite calcular E.
6.2.- DETERMINACION DE LAS PROPIEDADES DE ACUIFEROS CONFINADOS Y LIBRES POR ENSAYOS CON ABATIMIENTO ESCALONADO
Una de las ventajas que tiene la realización de ensayos con abatimiento escalonado, es que las propiedades del acuífero pueden determinarse con información de un solo pozo de observación.
Para calcular TD se parte de la ecuación 3.6, que aplicada a dos instantes A y B del escalón N,
(tB > tA ) permitirá expresar que la diferencia en abatimiento para un mismo punto del acuífero, resulta: (5)
de donde se obtiene:
Para calcular el coeficiente de almacenamiento, una vez obtenido TD, se toma el abatimiento SrN en el escalón N para un tiempo determinado y el abatimiento Sr(N-1) para otro tiempo determinado en el escalón N-1 y resolviendo las ecuaciones simultáneas resultantes quedará:(5)
Como todos los elementos de la ecuación 5.21 son conocidos, excepto E, con ella será posible calcular su valor.
Como ya se conocen los valores de TD y E se puede aplicar la ecuación general (ecuación 3.6), para a partir de un valor conocido de SrN en el mismo punto del acuífero que se ha venido analizando, poder calcular TT. Para hacer ese cálculo se puede utilizar también otra forma de expresar la ecuación general, que puede resultar más cómoda, y que es la siguiente:
El valor de ro a utilizar en las ecuaciones 3.6 ó 5.23 se calculará con la ecuación 4.9 para el tiempo t1 correspondiente al instante del escalón N para el cual se haya tomado el valor srN, o sea que:
De ese modo quedarán calculadas todas las propiedades del acuífero.
6.3.- DETERMINACION DE LAS PROPIEDADES DE ACUIFEROS SEMICONFINADOS CON ENSAYOS A CAUDAL CONSTANTE
Como se ha señalado, la ecuación 3.15 caracteriza el flujo impermanente no lineal en un acuífero semiconfinado y está expresada por:
El primer término del segundo miembro de la ecuación representa la componente lineal del abatimiento y el segundo término la componente turbulenta.
En este caso, para un tiempo determinado la diferencia de abatimiento entre dos puntos, 1 y 2 (el 1 más cercano que el 2 al pozo de bombeo) será lógicamente:
La solución de la ecuación 3.15 se hace, suponiendo inicialmente que no existe la componente turbulenta del abatimiento y determinando las propiedades del acuífero por alguno de los procedimientos desarrollados para el análisis del flujo lineal en acuífero semiconfinado.
Estas propiedades se determinarán para dos pozos de observación situados a distancias diferentes del pozo de bombeo y lo más cercano posible al mismo.
Si el flujo es no lineal, la diferencia de abatimiento entre dos puntos, observada para un tiempo determinado, tal como lo expresa la ecuación 5.26, será mayor que la diferencia entre las componentes lineales representada por el primer término del segundo miembro de la ecuación 5.26 calculadas con las propiedades obtenidas anteriormente para cada pozo. Si el flujo es lineal, la diferencia entre las componentes lineales será igual a la diferencia de abatimientos observada y lógicamente el segundo término del segundo miembro de la ecuación 5.26 será igual a cero. Si resulta que el flujo es lineal, el proceso de cálculo termina aquí y las propiedades calculadas anteriormente serán las que se buscaban. Si el flujo es no lineal, el proceso continúa y partiendo de la ecuación 5.26 se puede obtener:
de donde se puede determinar TT, ya que el resto de las variables son conocidas.
Determinada TT será posible calcular el valor constante de la componente turbulenta para cada punto del acuífero, utilizando lo expresado por el segundo término del segundo miembro de la ecuación 3.15, y de ese modo, tener los valores de la componente lineal para cada instante de tiempo, restándole a los valores observados de abatimiento el valor constante de la componente turbulenta.
Con los valores de las componentes lineales se recalcularán las propiedades del acuífero y una vez obtenidas se usarán en la ecuación 5.27, para recalcular TT, repitiendo el procedimiento hasta obtener el grado de aproximación que se desee entre dos iteraciones sucesivas.
Para el análisis del flujo lineal en acuíferos semiconfinados, Hantush ha desarrollado varios métodos. Uno de ellos utiliza las mediciones del abatimiento de un solo pozo de observación para resolver la componente lineal de la ecuación 5.25. Para ello se prepara un gráfico de tiempo-abatimiento en escala semilogarítmica.
En ese gráfico (Figura 5.7) aparece un llamado punto de inflexión p, para el cual se mantienen las siguientes relaciones:
donde: Ko es la función de Bessel modificada de segunda clase y orden cero; Sp, abatimiento en el punto de inflexión y Sm, abatimiento para condiciones de equilibrio observado o extrapolado.
donde: tp, tiempo correspondiente al punto de inflexión.
La pendiente de la representación gráfica del ensayo en el punto de inflexión, DSp está dada por:
y la relación entre el abatimiento y la pendiente en el punto de inflexión está representada por:
![]() Sp, corresponde también al abatimiento por ciclo logarítmico
Sp, corresponde también al abatimiento por ciclo logarítmico
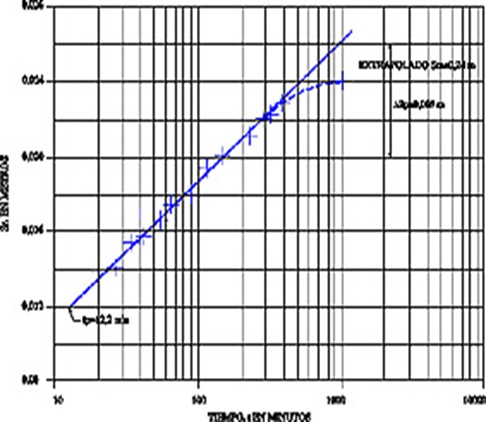
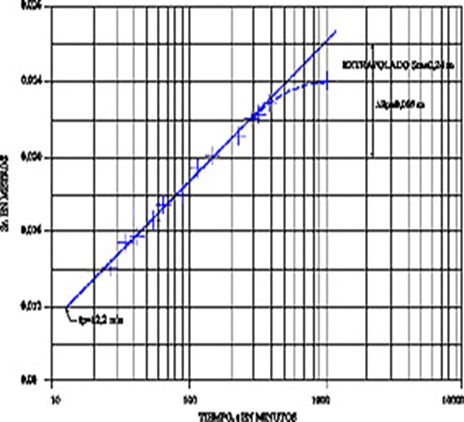
Fig. 5.7 Gráfico para el análisis del flujo semiconfinado
El procedimiento que se sigue para el análisis de los resultados del ensayo de bombeo en flujo lineal, según Kruseman (2) es el siguiente:
a) Se dibujan en papel semilogarítmico con el tiempo en la escala logarítmica, los valores del abatimiento para cada tiempo tomados de los resultados del ensayo.
b) Se determina el valor del abatimiento máximo, Sm, por extrapolación. Esto es posible solamente si el período de ensayo es lo suficietemente prolongado para que aparezcan los primeros síntomas de estabilización del abatimiento.
c) Se calcula Sp como Sm/2 y se localiza el punto de inflexión, p, en la curva de abatimiento con el valor de Sp.
d) Se determina el valor de tp, que corresponde al punto de inflexión, directamente del gráfico.
e) Se determina la pendiente ![]() Sp de la curva en el punto de inflexión. Esto es aproximadamente equivalente a la diferencia de abatimiento por ciclo logarítmico en la porción recta de la curva sobre la cual se encuentra el punto de inflexión.
Sp de la curva en el punto de inflexión. Esto es aproximadamente equivalente a la diferencia de abatimiento por ciclo logarítmico en la porción recta de la curva sobre la cual se encuentra el punto de inflexión.
f) Se introducen los valores Sp y ![]() Sp en la ecuación 5.31 y se determina r/B por interpolación en la tabla de la función ex K o(x) que aparece en el anexo II.
Sp en la ecuación 5.31 y se determina r/B por interpolación en la tabla de la función ex K o(x) que aparece en el anexo II.
g) Como se ha determinado r/B y se conoce el valor de r se puede calcular B.
h) Como Q, Sp, DSp y r/B son conocidos se calcula TD a partir de la ecuación 5.30 usando la tabla de la función e-x del anexo II o a partir de la ecuación 5.28 usando la tabla de la función Ko(x) del mismo anexo II.
i) Como se conocen TD, tp, r y r/B, se puede calcular E a partir de la ecuación 5.29.
j) Como TD y B son conocidos, se podrá calcular la resistencia hidráulica c' a través de la relación c' = B2/TD.
Si el flujo es lineal, se habrán obtenido los parámetros que lo caracterizan, pero para ello es necesario comprobar que efectivamente en las condiciones del ensayo, el flujo hacia el pozo es lineal.
Para comprobar la linealidad del flujo, ya se ha dicho que ésta se cumple si
Tomando un tiempo t, igual para ambos pozos de observación cercano al momento en que comienzan a manifestarse los primeros síntomas de estabilización del abatimiento, se calculan los valores de las funciones de pozo según el procedimiento siguiente:
1) Se calcula u con la ecuación 5.25 para cada punto.
2) Como r/B ya se conoce para cada punto, se determinan los valores de W(u,r/B)1 y W(u,r/B)2 utilizando el anexo I.
3) Se sustituyen estos valores en la ecuación 5.32 y si se cumple la igualdad o el primer miembro de la ecuación 5.32 es ligeramente menor que el segundo, el flujo será lineal. Si el primer miembro de la ecuación 5.32 es mayor que el segundo, el flujo será no lineal y se procederá como se describió anteriormente para esa situación.
Para hacer más comprensible el proceso de cálculo, esta situación se ilustra con un ejemplo.
6.4.- EJEMPLO DE DETERMINACION DE PROPIEDADES DE UN ACUIFERO SEMICONFINADO EN EL CASO MÁS GENERAL NO LINEAL
Los resultados del ensayo de un acuífero semiconfinado con un caudal constante de 75 m3/h (1,25 m3/min) en dos pozos de observación aparecen en la tabla No. 5.4.
Los gráficos de tiempo abatimiento para ambos pozos están representados en la figura 5.8 para el pozo No. 1 y en la figura 5.9 para el pozo No. 6.
Pozo de observación No. 1 (r1 = 10,23 m)
Del gráfico de la figura 5.8 Sm = 2,60
TABLA No. 4
| Pozo de observación No. 1 | Pozo de observación No. 2 | ||||||
| Tiempo | Abatim. | Tiempo | Abatim. | Tiempo | Abatim. | Tiempo | Abatim. |
| 1 | 0,83 | 150 | 2,21 | 1 | 0,31 | 240 | 1,74 |
| 2 | 1,08 | 180 | 2,26 | 3 | 0,65 | 300 | 1,79 |
| 3 | 1,20 | 240 | 2,31 | 5 | 0,79 | 360 | 1,82 |
| 4 | 1,29 | 300 | 2,37 | 7 | 0,86 | 420 | 1,85 |
| 5 | 1,36 | 360 | 2,39 | 10 | 0,95 | 500 | 1,89 |
| 7 | 1,44 | 420 | 2,41 | 15 | 1,06 | 600 | 1,95 |
| 10 | 1,53 | 500 | 2,45 | 20 | 1,14 | 700 | 1,97 |
| 15 | 1,63 | 600 | 2,52 | 25 | 1,20 | 800 | 1,99 |
| 20 | 1,71 | 700 | 2,55 | 30 | 1,24 | 1000 | 1,99 |
| 25 | 1,77 | 800 | 2,56 | 40 | 1,32 | 1200 | 1,99 |
| 30 | 1,82 | 1000 | 2,56 | 60 | 1,42 | 1500 | 2,03 |
| 40 | 1,89 | 120 | 2,56 | 90 | 1,52 | ||
| 60 | 1,99 | 1500 | 2,60 | 120 | 1,58 | ||
| 90 | 2,08 | 150 | 1,64 | ||||
| 120 | 2,15 | 180 | 1,69 |
Utilizando la ecuación 5.31 resulta:
En el anexo II, el valor 5,64 es mayor que todos los tabulados. Luego, r/B << ALTO PUEDE &BULL;).
Cálculo de TD a partir de la ecuación 5.30:
No se puede calcular E por el procedimiento establecido
Fig.5.8. Gráfico de tiempo abatimiento, pozo de observador No.1
Fig. 5.9 Gráfico de tiempo abatimiento, pozo de observador No.6
Pozo de observación No. 6 (r6 = 24,62m)
Del gráfico de la figura 5.9 Sm = 2,03 m
tp = 9,8 minutos (figura 5.9)
Utilizando la ecuación 5.31, resulta:
En el anexo II, interpolando, se obtiene r/B = 0,0135 luego B = r/0,0135 = 24,62/0,0135 = 1823,7 m.
Cálculo de TD a partir de la ecuación 5.30
Para r/B = 0,0135 e-r/B = 0,9875 (Anexo I)
Cálculo de E a partir de la ecuación 5.29
Reconocimiento del carácter del flujo (lineal o no lineal)
El tipo de flujo se determina aplicando la ecuación 5.32 a un tiempo cercano a la estabilización. Tomando t = 490 minutos se tiene:
Sr1 = 2,465 m
Sr2 = 1,90 m
Calculando u por la ecuación 5.25 para cada punto.
Como no se pudo calcular E para el punto 1 se usará el mismo valor que se obtuvo para el punto 6.
Interpolando en el anexo I se obtiene:
W(u,r/B)1 = 10,09
Para el punto 6
Interpolando en el anexo I se obtiene:
W(u,r/B)6 = 8,03
Analizando los miembros de la ecuación 5.32 resulta
Sr1 - Sr2 = 2,465 - 1,90 = 0,565 m
Usando para TD la media de los dos lugares o sea TD = 0,433 m2/min. resulta:
Se ve claramente que Sr1 - Sr2 es mayor que la diferencia entre las componentes lineales. Luego, de acuerdo con la ecuación 5.27
Con este valor de TT se calcula el valor de la componente turbulenta del abatimiento en cada pozo, que como se sabe es constante a través del tiempo, utilizando la expresión de la componente turbulenta.
Para el pozo No. 6 (r6 = 24,62)
De modo que la componente lineal del abatimiento estará representada por una línea paralela a la que representa los datos Sr-log t del ensayo, situada a la distancia ST por debajo de ésta.
Así, para el pozo No. 1 la línea L-L de la figura 5.8 representará la componente lineal y sobre ella deben hacerse los cálculos para determinar los parámetros del acuífero semiconfinado. De modo que se tendrá:
Utilizando la ecuación 5.31 resulta:
En el anexo II, el valor 5,30 es mayor que todos los tabulados. Luego r/B<<0,010. PUEDE VALOR PERO CALCULAR SE SU ES MUY ALTO
Cálculo de TD a partir de la ecuación 5.30
No se puede calcular E por el procedimiento establecido.
Para el pozo No. 6 la línea L1-L1 de la figura 5.9 representará la componente lineal y sobre ella deben hacerse los cálculos para determinar los parámetros del acuífero semiconfinado. De modo que se tendrá:
En el anexo II, interpolando se obtiene r/B=0,0145. Luego B=r/0,0145=24,62/0,0145=1697,9 m. Para el de TD se parte de la ecuación 10
para r/B = 0,0145 e-r/B = 0,9855 (Anexo II)
Cálculo de E a partir de la ecuación 5.29
Como se ha probado, el flujo es no lineal por lo que corresponde calcular los términos de la ecuación 5.27 para un tiempo t=490 minutos para hacer el ajuste correspondiente.
Diferencia entre los abatimientos observados:
Sr1 - Sr2 = 2,465 - 1,90 = 0,565
Para calcular la diferencia entre las componentes lineales, se determina primero el valor de u por la ecuación 5.25 para cada punto.
Para el punto 1, como no se puede calcular E, se utilizará el valor obtenido en esta segunda aproximación para el punto 6, o sea,
E=2,386.10-4 luego:
Interpolando en el anexo I se obtiene:
W(u,r/B)1 = 9,88
Para el punto 6
Interpolando en el anexo I, se obtiene:
W(u,r/B)6 = 7,817
Luego usando TD promedio = 0,4326 la diferencia de componentes lineales es:
Entonces de acuerdo con la ecuación 5.27
La diferencia entre el valor obtenido anteriormente para TT y el obtenido ahora es muy pequeña, por lo que se puede dar por terminado el proceso de ajuste y las propiedades del acuífero serán:
TD = 0,4326 m2/min (promedio)
TT = 0,1572 m2/min (promedio)
E = 2,386.10-4 (para el punto 6)
B=1697,9 m (para el punto 6)
c' = 4617,1 días (para el punto 6)
7.- DETERMINACION DE LA ECUACION CARACTERISTICA DE UN POZO DE BOMBEO
Ha sido costumbre hasta el momento expresar la ecuación característica de los pozos de bombeo por expresiones de la forma propuesta por Rorabaugh (10), o sea:
SW = BQ + Cqy (5.33)
que puede reducirse a la que había propuesto anteriormente Jacob (3) haciendo y=2, es decir que:
SW = BQ + CQ2 (5.34)
Ambas expresiones parten del supuesto teórico de que BQ representa el abatimiento que se produciría en el pozo debido a la resistencia del acuífero para condiciones de flujo lineal sin tener en cuenta la estructura del pozo y que CQy (ó CQ2) representa las pérdidas de carga debidas a los demás factores.
A pesar de que tanto la formulación de Jacob como la de Rorabough suponen inicialmente la variación con el tiempo del coeficiente B, en la práctica lo que se determina es el valor de dicho coeficiente para condiciones de equilibrio, lo que limita indiscutiblemente el uso de la ecuación.
Tal como se ha visto en el epígrafo 1.6 al analizar la estructura del pozo, las componentes del abatimiento no responden en realidad a este sencillo esquema y teniendo en cuenta además el hecho de que el flujo en el acuífero puede ser no lineal, Pérez Franco (7) ha propuesto una nueva ecuación característica para el pozo de bombeo que ya se ha presentado como ecuación 3.8, o sea:
Esta ecuación tiene la ventaja de que permite predecir el abatimiento para cualquier tiempo a partir del inicio del bombeo y que tiene en cuenta las condiciones más generales de flujo y de variaciones en las condiciones físicas alrededor del pozo y que no se necesita llegar a la estabilización del pozo para determinarla.
La ecuación característica del pozo de bombeo puede determinarse a partir de dos ensayos a caudal constante con caudales diferentes o de un ensayo con abatimiento escalonado con al menos tres escalones.
7.1.- DETERMINACION DE LOS COEFICIENTES DE LA ECUACION CARACTERISTICA A PARTIR DE ENSAYOS A CAUDAL CONSTANTE
Como se ha señalado anteriormente, para determinar los coeficientes de la ecuación característica a partir de ensayos a caudal constante, es necesario haber realizado al menos dos pruebas con caudales diferentes.
El cálculo de TD puede hacerse aplicando la ecuación 3.8 a dos tiempos diferentes, tc y tB (tc >tB) para un mismo caudal, de donde resulta:
Como se sabe, la ecuación 5.38 representa una línea recta en un acuífero semilogarítmico de tiempo-abatimiento y el valor de TD podrá también calcularse gráficamente por el procedimiento acostumbrado.
Una vez calculado TD, para determinar los coeficientes KLW y DW se aplicará la ecuación 3.8 a un mismo tiempo tA a dos caudales diferentes, Q1 y Q2 de donde resulta:
En las ecuaciones 5.39 y 5.40 se conocen SW1, SW2, tA, TD, Q1, y Q2, por lo que será posible calcular KLW y DW simultáneamente de ambas ecuaciones.
7.2.- DETERMINACION DE LOS COEFICIENTES DE LA ECUACION CARACTERISTICA A PARTIR DE ENSAYOS CON ABATIMIENTO ESCALONADO
Pérez Franco (8) ha demostrado que el abatimiento en un pozo de bombeo en el escalón N durante un ensayo con abatimiento escalonado puede expresarse como:
Como en esta ecuación aparecen todos los elementos que permiten expresar debidamente la ecuación característica, a partir de ella con los datos de abatimiento escalonado se calcularán TD, KLW y DW.
Para calcular TD se aplica la ecuación 5.41 a los resultados obtenidos en el ensayo, para dos tiempos diferentes, tA y tB (tA > tB) en el escalón N. De modo que resultará:
de la cual puede deducirse TD
Los valores de DW y KLW conocida TD, pueden determinarse aplicando la ecuación 5.41 a tiempos seleccionados en dos escalones consecutivos, obteniéndose de ese modo, dos ecuaciones que en conjunto permitirán calcular ambos coeficientes, quedando así definidos los tres parámetros necesarios para expresar la ecuación característica del pozo.
Conclusiones
Ø La aplicación de metodologías acordes en la evaluación de yacimientos de agua subterránea, permite establecer los parámetros hidrogeológicos del acuífero, establecer las condiciones del entorno, evaluar la potencialidad del reservorio, predecir el comportamiento del agua subterránea ante una demanda determinada y sobre todo determinar la ubicación de futuras obras similares a la existente (dren subsuperficial) en un radio tal que no existan interferencias
Ø Las formaciones geológicas en que se acumula el agua subterránea y que son capaces de cederla reciben el nombre de acuíferos. Los acuíferos sirven como conductos de transmisión y como depósitos de almacenamiento
Ø Los acuicludos o acuicierres (del latín claudere = cerrar) son formaciones geológicas impermeables que contienen agua, pero que no la transmiten, haciendo de este modo imposible su explotación
Ø Los acuíferos formados por depósitos no consolidados, están constituidos por materiales sueltos, fundamentalmente, arenas, gravas o mezclas de ambas de origen geológico muy diverso.
Ø
Autores:
Watanabe Cabrera, Jorge A.
Chávarri Cueva, Melissa.
Tafur Terán, Alan A.
Pérez Castañeda, Alan R.
Fernández Julca, Javier E.
Docente: Ing. Wilver Morales Céspedes







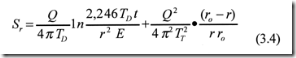













![clip_image249[1] clip_image249[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEibeV10XRnB47u3gHX-7foUWbt5wbipH0E1DJ1kdB6W0nUVfw8b87h8aVg2WaXxI20wnVNgKNIuDZ1WTHGp-BTd-z4bAMTy5EWxFfXAC8WBo8VIUlRvTocS7VeGP5c6O1IQOVcT/?imgmax=800)
![clip_image258[1] clip_image258[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjaCXxwSuDqYZjJuIyGJCgXlusQzwsl3b6mL8nGjQA9w0OwAKQNFjYTTKmoWM5QELcmYAZ7XL-iXHOHG21-ifBnujqc3u08eQIACZystAIZ4Qv3u_wZVNzCtllLEXt2TwVkhTlk/?imgmax=800)



![clip_image265[1] clip_image265[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEju3xkgCFpUQFuAq5MHvUfzbWwzgM7nHzN3ArYgceCNII3CoY6J3slVmeYiNJBW5Yeb4DcLLt7UcI9VsWEyrnPlCZvGeFc5MH7VIu7jLX8KyNt47yNiuxHouaNPRAviqDNEjiJw/?imgmax=800)