Tracción en Metales

1.1 OBJETIVOS

1.1.1 Objetivo general

Analizar el comportamiento de diversos materiales metálicos al ser sometidos a un esfuerzo de tensión uniaxial.

1.1.2.Objetivos específicos

Calcular la resistencia a la tracción de cada uno de los materiales ensayados.

El estudiante debe mencionar tres objetivos específicos más. Ver actividades a realizar.

1.2. GENERALIDADES

El ensayo se realiza en una Máquina Universal (figura1.2) y la operación consiste en someter una probeta (ver figura 1.1) a una carga monoaxial gradualmente creciente (es decir, estática) hasta que ocurra la falla.

Las probetas para ensayos de tensión se fabrican en una variedad de formas. La sección transversal de la probeta puede ser redonda, cuadrada o rectangular. Para la mayoría de los casos, en metales, se utiliza comúnmente una probeta de sección redonda. Para láminas y placas usualmente se emplea una probeta plana.

Figura 1.1 Probeta para ensayo de tracción

La transición del extremo a la sección reducida debe hacerse por medio de un bisel adecuado para reducir la concentración de esfuerzos causados por el cambio brusco de sección.

El esfuerzo axial s en el espécimen de prueba (probeta) se calcula dividiendo la carga P entre el área de la sección transversal (A):

FIGURA 1.2 MÁQUINA PARA ENSAYO DE TRACCIÓN

Cuando en este cálculo se emplea el área inicial de la probeta, el esfuerzo resultante se denomina esfuerzo nominal (esfuerzo convencional o esfuerzo de ingeniería). Se puede calcular un valor más exacto del esfuerzo axial, conocido como esfuerzo real.

La deformación unitaria axial media se determina a partir del alargamiento medido “d“entre las marcas de calibración, al dividir d entre la longitud calibrada L₀. Si se emplea la longitud calibrada inicial se obtiene la deformación unitaria nominal (e).

Después de realizar una prueba de tensión y de establecer el esfuerzo y la deformación para varias magnitudes de la carga, se puede trazar un diagrama de esfuerzo contra deformación. Tal diagrama es característico del material y proporciona información importante acerca de las propiedades mecánicas y el comportamiento típico del material.

En la figura 1.3 se muestra el diagrama esfuerzo deformación representativo de los materiales dúctiles. El diagrama empieza con una línea recta desde O hasta A. En esta región, el esfuerzo y la deformación son directamente proporcionales, y se dice que el comportamiento del material es lineal. Después del punto A ya no existe una relación lineal entre el esfuerzo y la deformación, por lo que el esfuerzo en el punto A se denomina límite de proporcionalidad. La relación lineal entre el esfuerzo y la deformación puede expresarse mediante la ecuación s = Ee, donde E es una constante de proporcionalidad conocida como el módulo de elasticidad del material. El módulo de elasticidad es la pendiente del diagrama esfuerzo-deformación en la región linealmente elástica y su valor depende del material particular que se utilice.

Figura 1.3. Diagrama esfuerzo-deformación de materiales dúctiles en tensión (fuera de escala)

La ecuación s = Ee se conoce comúnmente como ley de Hooke.

Al incrementar la carga más allá del límite de proporcionalidad, la deformación empieza a aumentar más rápidamente para cada incremento en esfuerzo. La curva de esfuerzo deformación asume luego una pendiente cada vez más pequeña, hasta que el punto B de la curva se vuelve horizontal. A partir de este punto se presenta un alargamiento considerable, con un incremento prácticamente inapreciable en la fuerza de tensión (desde B hasta C en el diagrama). Este fenómeno se conoce como cedencia o fluencia del material, y el esfuerzo en el punto B se denomina esfuerzo de cedencia o punto de cedencia (o bien, esfuerzo de fluencia o punto de fluencia). En la región de B hasta C, el material se vuelve perfectamente plástico, lo que significa que puede deformarse sin un incremento en la carga aplicada.

Después de sufrir las grandes deformaciones que se presentan durante la fluencia en la región BC el material empieza a mostrar un endurecimiento por deformación. Durante este proceso, el material sufre cambios en sus estructuras cristalina y atómica, lo que origina un incremento en la resistencia del material a futuras deformaciones. Por tanto, un alargamiento adicional requiere de un incremento en la carga de tensión, y el diagrama esfuerzo-deformación toma una pendiente positiva desde C hasta D. Finalmente la carga alcanza su valor máximo y el esfuerzo correspondiente (en el punto D) se denomina esfuerzo último. De hecho, el alargamiento posterior de la barra se acompaña de una reducción en la carga y finalmente se presenta la fractura en un punto E, tal como se indica en el diagrama.

Se presenta una contracción lateral de la muestra cuando se alarga, lo que origina una reducción en el área de la sección transversal. La reducción en el área es muy pequeña como para tener un efecto apreciable en el valor de los esfuerzos calculados antes del punto C, pero más allá de este punto la reducción comienza a modificar el perfil del diagrama. Desde luego, el esfuerzo real es mayor que el esfuerzo nominal debido a que se calcula con un área menor.

En la cercanía del esfuerzo último, la disminución del área se aprecia claramente y ocurre un estrechamiento pronunciado de la barra, conocido como estricción. Si para el cálculo del esfuerzo se emplea el área de la sección transversal en la parte estrecha del cuello ocasionado por la estricción, la curva real esfuerzo-deformación seguirá la línea punteada CE’. La carga total que puede resistir la probeta se ve efectivamente disminuida después de que se alcanza el esfuerzo último (curva DE), pero esta disminución se debe al decremento en área de la probeta y no a una pérdida de la resistencia misma del material. En realidad, el material soporta un aumento de esfuerzo hasta el punto de falla (punto E’).

Sin embargo, con fines prácticos la curva esfuerzo-deformación convencional OABCDE, basada en el área transversal original de la muestra y que, por lo tanto, se calcula fácilmente, suministra información satisfactoria para emplearla en el diseño. La ductilidad de un material a tensión puede caracterizarse por su alargamiento total y por la disminución de área en la sección transversal donde ocurre la fractura.

La elongación porcentual se define como sigue:

donde L_o es la longitud calibrada original y L_f es la distancia entre las marcas de calibración al ocurrir la fractura.

La reducción porcentual de área mide el valor de la estricción que se presenta y se define como sigue:

Donde A_o es el área original de la sección transversal y A_f es el área final en la sección de la fractura.

Los materiales que fallan en tensión a valores relativamente bajos de deformación unitaria se clasifican como materiales frágiles.

En este ensayo las propiedades usualmente determinadas son: La resistencia a la cedencia (punto de cedencia), la resistencia a la tensión, la ductilidad (El alargamiento y la reducción de área), el módulo de elasticidad y el tipo de fractura.

1.3 MATERIAL Y EQUIPO A UTILIZAR

- Máquina Universal (Figura 1.2).

- Aditamentos para el ensayo de tracción.

- Indicador de Carátula.

- Calibrador.

- Pinzas, destornillador.

- Probetas metálicas.

1.4 PROCEDIMIENTO

1.4.1. Anote en la tabla 1.1 las medidas correspondientes a cada una de las probetas a ensayar.

1.4.2. Prepare la máquina para ensayos a tracción: coloque los aditamentos correspondientes para sujetar la probeta.

1.4.3. Enrosque la probeta en los respectivos sujetadores, dejando que sobresalgan aproximadamente dos hilos de rosca en cada extremo.

1.4.4. Aplique una pequeña precarga a la probeta hasta que el movimiento de la aguja en el manómetro sea inminente.

1.4.5. Gradúe el indicador (Deformímetro) en "cero".

1.4.6. Aplique carga de una manera continua y lenta y vaya tomando lecturas en el manómetro de acuerdo a la tabla 1.2.

1.4.7. Una vez ocurra la falla, retire las partes de la probeta ensayada, preséntelas y mida el diámetro de la sección de rotura así como la nueva longitud entre los puntos de calibración.

1.4.8. Coloque una nueva probeta en la máquina y repita los pasos anteriores.

Nota: De acuerdo al diseño de la máquina, el valor de presión leído en el manómetro se debe multiplicar por 5.52 para obtener el valor de fuerza aplicada sobre la probeta, esto es: F = 5.52*Pr.; Fuerza en Kg.-f y presión en psi.

1.5. ACTIVIDADES A REALIZAR

1.5.1. Antes de la práctica

1.5.1.1. Clases de fracturas en materiales metálicos sometidos a tracción (Realice gráficas).

Las típicas clases de fracturas en materiales metálicos son fractura dúctil, fractura frágil, fractura por fatiga, fractura por Creep y fractura debida al medio ambiente.

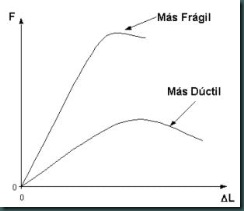
1.5.1.2. Características del diagrama esfuerzo-deformación para materiales frágiles (Realice la gráfica). Compare con el diagrama para materiales dúctiles.

En materiales frágiles, incluyendo muchos cerámicos, el esfuerzo de cadencia, la resistencia a la tensión y el punto de ruptura tienen un mismo valor. En muchos materiales frágiles no se puede efectuar con facilidad el ensayo de tensión debido a la presencia de defectos de superficie. Mientras que en los materiales dúctiles la curva esfuerzo-deformación generalmente pasa por un valor máximo, este esfuerzo máximo es la resistencia del material a la tensión. La falla ocurre a un esfuerzo menor después de que el encuellamiento ha reducido el área de la sección transversal que soporta la carga.

1.5.1.3. ¿Influye la velocidad de aplicación de la carga en los ensayos? Explique.

La velocidad con que se la aplica la carga a la probeta en el ensayo de tracción si tiene que ver porque el material no se va a comportar de la misma manera como se comporta cuando se le aplica una carga lenta, ósea, que no va a tener la misma zona elástica y el esfuerzo ultimo puede no ser el mismo que cuando se le aplica una carga lenta.

1.5.2. Otras

1.5.2.1. Mencione tres objetivos específicos.

· Conocer y aprender como utilizar los diferentes materiales y equipos que hay en el laboratorio.

· Observar el comportamiento de los materiales al aplicársele una carga.

· Reconocer el tipo de material por medio de la grafica esfuerzo-deformación.

1.5.2.2 Registre en las tablas 1.1 y 1.2 los datos de acuerdo con el procedimiento.

Están después de las actividades a realizar.

1.5.2.3. ¿Influye la temperatura en los resultados de las pruebas de tracción? Explique.

La temperatura si influye en este ensayo a tracción ya que las propiedades a la tensión dependen de la temperatura. El esfuerzo de cadencia, la resistencia a la tensión y el módulo de elasticidad disminuyen a temperaturas más altas, en tanto que, por lo general, la ductilidad se incrementa.

1.5.2.4. Describa el procedimiento realizado en el taller de la UTB. Para la obtención de las probetas a ensayar.

El procedimiento es el siguiente: primero tomamos las medidas de las probetas de acero y aluminio y las anotamos en la tabla correspondiente, mas tarde nos explicaron como funciona la maquina y se procedió a la colocación de las probetas en la maquina dejando dos hilos por fuera en cada lado y se le aplica una pequeña carga asta que quedara completamente tesa. Después procedimos a aplicarle la carga y la toma de datos asta que se rompió la probeta, después que se rompiera la probeta se procedió a quitarla de la maquina y a tomarle las nuevas lecturas como el área por donde se rompió y el nuevo largo que obtuvo después de la ruptura y este mismo procedimiento se utilizo para la las dos probetas

1.5.2.5. Dibuje en papel milimetrado y en una misma gráfica, las curvas esfuerzo-deformación para cada uno de los materiales ensayados. Analícelas y compárelas.

1.5.2.6. Calcule la resistencia a la cedencia de cada uno de los materiales ensayados. Analice y compare.

Se calcula midiendo 0.002 en el eje x. se pasa un alinea paralela al eje y en al grafica esfuerzo-deformación y por donde corte es al cadencia del material.

1.5.2.7. Calcule la resistencia a la tensión de cada uno de los materiales ensayados. Analice y compare.

La última tensión que resistió el aluminio fue de 16288.8N y la ultima tensión que resistió el acero fue de 54093N

1.5.2.8. Calcule la ductilidad de cada uno de los materiales ensayados. Analice y compare.

· Aluminio:

% alargamiento = 100 * lb - l0 / l0

= 100 *17.23 – 14 / 14

% alargamiento = 23 mm

· Acero

% alargamiento = 100 * lb - l0 / l0

= 100 * 14.34 – 14 / 14

% alargamiento = 2.4285 mm

1.5.2.9. Calcule el módulo de elasticidad a cada uno de los materiales ensayados. Analice y compare.

· Aluminio:

P1 (0,0) P2 (2037.82, 0.0893)

m = 22.826 GPa

· Acero

P1 (0,0) P2 (10763.23, 0.0367)

m = 293.27 GPa

1.5.2.10. Compare los valores hallados para los módulos de elasticidad con los tabulados. Halle porcentaje de error y explique.

El porcentaje de error nos da mucho mayor porque las condiciones en que trabajamos no fueron las mas optimas para hacer el ensayo, no solo las condiciones sino también la forma en que se tomaron las medidas que fueron redondeadas y también en los cálculos que se redondeaban sin tener en cuenta los decimales y al comernos los decimales en cada calculo el porcentaje de error se va haciendo cada ves mayor.

1.5.2.11. ¿Qué clase de fractura presentaron los materiales ensayados?

Se presento una fractura simple en ambos materiales donde el material se dividió en dos partes como respuesta a una tensión que puede ser estática, constante o puede ir variando lentamente con el tiempo.

Nota: Los valores de las propiedades a determinar se deben calcular para cada una de las probetas ensayadas y luego obtener el promedio de acuerdo a la cantidad de probetas.

Tabla 1.1. Medidas de las probetas

MATERIAL	L (mm)	d (mm)	LR (mm)	LO (mm)	dO (mm)	df (mm)	Lf (mm)	AREA (mm2)
ALUMINIO	14	1.9	4.1	5.6	1.3	0.66	11.22	1.3273
ACERO	14	1.85	2.94	8.16	0.8	0.72	14.34	0.5026

Tabla 1.2 Material

ALUMINIO ACERO

d 10-2 mm	P psi	P N	s N/mm2	e		d 10-2 mm	P psi	P N	s N/mm2	e
0	0	0	0	0.0178	0	0	0	0	0
10	0	0	0	0.0357	10	0	0	0	0.0122
20	0	0	0	0.0535	20	20	1081.92	2152.65	0.0245
30	0	0	0	0.0714	30	100	5409.6	10763.23	0.0367
40	10	540.96	407.56	0.0892	40	200	10819.2	21526.46	0.0490
50	50	2704.8	2037.82	0.1071	50	250	13524	26908.1	0.0612
60	100	5409.6	4075.64	0.125	60	300	16228.8	32289.7	0.0735
70	250	8114.4	6113.46	0.1428	70	350	18933.6	37671.30	0.0857
80	275	14876.4	11208.02	0.1607	80	400	21638.4	43052.92	0.0980
90	300	16228.8	12226.92	0.1785	90	550	29752.8	59197.8	0.1102
100	325	17581.2	13245.83	0.2142	100	700	37867.2	75342.62	0.1125
120	350	18933.6	14264.74	0.25	120	850	45981.6	91487.46	0.1470
140	360	19474.56	14672.31	0.2857	140	950	51391.2	102250.7	0.1716
160	370	20015.52	15079.88	0.3214	160	1000	54096	107632.31	0.1960
180	400	21638.4	16032.57	0.3561	180	1050	56800.8	113013.93	0.2205
200	400	21638.4	16032.57	0.3928	200	1100	59505.6	118395.54	0.2450
220	425	22990.8	17321.48	0.4285	220	1150	62210.4	123777.2	0.2696
240	450	24343.2	18340.39	0.4642	240	1150	62210.4	123777.2	0.2941
260	450	24343.2	18340.39	0.5	260	1150	62210.4	123777.2	0.3186
280	450	24343.2	18340.39	0.5357	280	1100	62210.4	123777.2	0.3431
300	460	24884.16	18747.95	0.625	300	1050	59505.6	118395.54	0.3676
350	460	24884.16	18747.95	0.71452	350	1000	54096	107632.31	0.4289
400	460	24884.16	18747.95	0.8035	400
450	470	25425.12	19155.52	0.8928	450
500	470	25425.12	19155.52	0.9821	500
550	470	25425.12	19155.52	1.0714	550
600	470	25425.12	19155.52	1.1607	600
650	450	24343.2	18340.39	1.025	650
700	450	24343.2	18340.39	1.3392	700
750	450	24343.2	18340.39	1.4285	750
800	450	24343.2	18340.39	1.5178	800
850	450	24343.2	18340.39	1.6071	850
900	300	16228.8	12226.92	1.725	900

1.6 CÁLCULOS TIPO.

Los tipos de cálculos que se manejaron fueron los siguientes:

El cálculo para las áreas de las probetas del acero y la de aluminio

Otro tipo de calculo fue el de pasar los datos de P que teníamos en psi pasarlos a N y para eso tenemos que multiplicar por 5.52 esta formula vale tanto para le acero como para el aluminio

Ejemplo para el aluminio

Otro calculo que se realizo fue para el esfuerzo; la formula es valida para los dos materiales

El A es la sección transversal del material

Ejemplo con un valor de P=2208N para el aluminio

Otro tipo de cálculo es de deformación unitaria; la formula es valida para los dos materiales

Donde L_o es igual a la longitud calibrada que esta entre las marcas de calibración

Ejemplo con un valor de δ=30*10^-2mm para el aluminio

Otro cálculo es el que se hizo para hallar el modulo de elasticidad

1.7 CONCLUSIONES Y RECOMENDACIONES.

Con la realización del ensayo de tracción nos dimos cuenta del comportamiento de ciertos materiales como el acero y el aluminio, cuando estos son sometidos a una tensión. Por otra parte concluimos que el aluminio es más frágil que el acero. Y por ultimo los materiales no se rompieron por la mitad debido a la estructura del material.

UNIVERSIDAD TECNOLÓGICA DE BOLÍVAR

CARTAGENA D.T. Y C.