El presente trabajo tiene el objetivo de realizar un estudio y análisis de los pórticos de acero como estructuras principales para la construcción de naves industriales. En concreto se trata de proponer perfiles de acero de sección e inercia variables, para de esta manera dotar al pórtico de área y rigidez suficientes en las zonas de mayores esfuerzos y restar resistencia en las zonas menos solicitadas. De esta manera se consigue un reparto más equitativo de tensiones a lo largo de la barra y además ahorramos acero en zonas innecesarias, lo cual es el objetivo fundamental de un ingeniero.
El problema está enfocado de la siguiente manera:
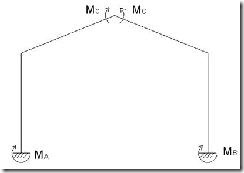
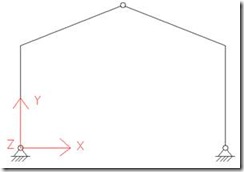
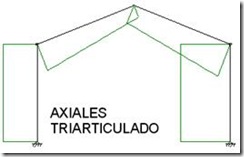
En primer lugar he buscado el perfil de inercia variable óptimo para las barras de un pórtico de acero triarticulado, es decir, semidinteles articulados entre sí y apoyos de soportes también articulados, de manera que en ellos se anulan los momentos flectores y por tanto no se transmiten a cimentación. La ventaja que tiene trabajar sobre este tipo de estructura es que es de naturaleza isostática y por tanto es fácil analizarla aplicando las leyes de la estática sin ser necesario un predimensionamiento previo.
Una vez obtenido el perfil óptimo para el pórtico antes mencionado, he intentado obtener unas leyes de transformación que permitan aplicar los resultados obtenidos a otros tipos de estructuras más usadas y constructivamente mejores, en este caso, pórticos biarticulados (apoyos articulados y unión rígida de semidinteles) y pórticos biempotrados (apoyos empotrados y unión rígida de semidinteles). El no estudiar directamente estos modelos estructurales se debe a que son hiperestáticos, es decir, tenemos más incógnitas de reacción que ecuaciones de la estática aplicables, por tanto necesitan un predimensionamiento de los perfiles a utilizar, lo cual conduce a sucesivas iteraciones que hacen el cálculo más tedioso.
Finalmente se termina discutiendo la viabilidad de cada pórtico analizando ventajas e inconvenientes de cada uno de ellos y aportando algunas sugerencias finales.
2) ANÁLISIS ISOSTÁTICO DEL PÓRTICO TRIARTICULADO
2.1) Descripción de la estructura a analizar
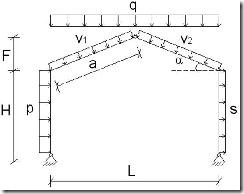
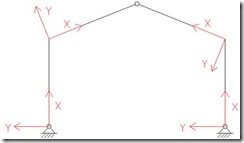
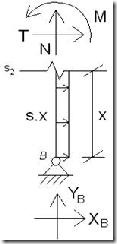
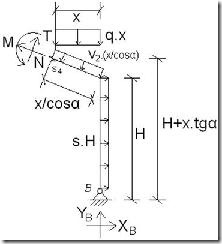
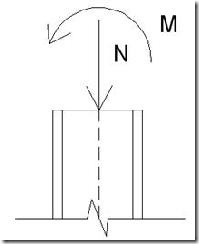
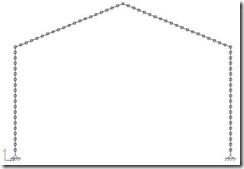
El pórtico triarticulado como he comentado anteriormente está apoyado sobre cimentación mediante articulaciones, así como los dos semidinteles también están articulados entre sí (ver Figura 1).
Figura 1. Pórtico triarticulado
Los apoyos articulados ideales no son fáciles de llevar a la práctica, ya que es difícil dar seguridad y firmeza a la estructura permitiendo a su vez que los nudos tengan libertad de giro (ver Figuras 2 y 3).
Figura 2. Apoyo articulado (Rótula). Figura 3. Apoyo semiarticulado
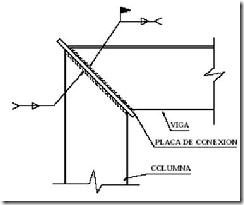
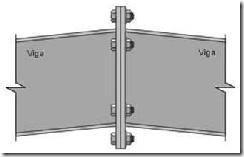
Las uniones del soporte con el semidintel son rígidas. Esta se consigue ensamblando ambas barras de manera que estas se muevan de manera solidaria cuando se produzcan desplazamientos (ver Figuras 4 y 5).
Figura 4. Unión rígida soporte-semidintel mediante placas atornilladas.
Figura 5. Unión rígida soporte-semidintel mediante placas soldadas.
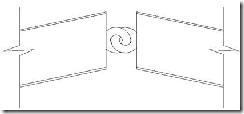
En cuanto a las uniones entre semidinteles, la articulación se suele ejecutar con un enlace sin reforzar (sin cartelas rigidizadoras) o soldando a ambas caras de los perfiles unas anillas que conexionen los dinteles pero permitan el giro del nudo (ver Figura 6).
Figura 6. Unión articulada entre semidinteles.
Una vez descrita la estructura a estudiar, ya podemos comenzar con su análisis.
2.2) Hipótesis de carga
El estudio de las acciones será realizado según la Norma de Acciones en la edificación (AE-88), llegando finalmente a unas cargas distribuidas linealmente a lo largo de las barras como se muestra a continuación.
La nomenclatura de las cargas es la siguiente:
q = Cargas gravitatorias (constantes + nieve)
p = Carga de presión de viento lateral sobre cerramiento
s = Carga de succión de viento lateral sobre cerramiento
v1 = Carga de viento en cubierta a barlovento
v2 = Carga de viento en cubierta a sotavento
2.3) Cálculo de las reacciones en los apoyos
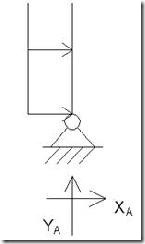
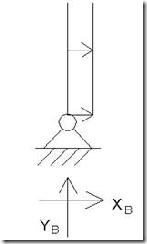
Una vez conocido el esquema de carga de la estructura ya se pueden calcular las reacciones en los apoyos, YA, YB, XA, XB. En este caso no tenemos momento ya que nos encontramos ante un nudo articulado.
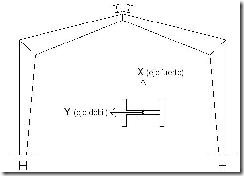
Para el cálculo de dichas reacciones aplicamos las ecuaciones de la estática, pero antes definiremos los ejes globales y locales del pórtico así como el convenio de signos:
EJES GLOBALES DE LA ESTRUCTURA
EJES LOCALES DE CADA BARRA
Entonces:
Después de realizar los cálculos se obtiene:
2.4) Cálculo de las leyes de esfuerzos internos para cada barra
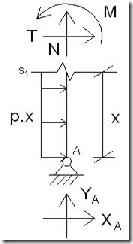
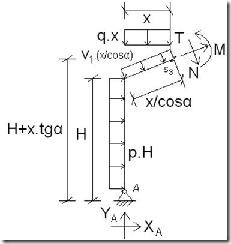
Conocidas las reacciones en la base de los soportes, ya podemos realizar el análisis de las leyes de esfuerzos internos. Para ello haremos los diagramas de cuerpo libre de cada una de las barras del pórtico:
SOPORTE IZQUIERDO M = Momento flector
N = Esfuerzo axial
T = Esfuerzo cortante
SOPORTE DERECHO
SEMIDINTEL IZQUIERDO
SEMIDINETL DERECHO
3) ECUACIÓN DE GEOMETRÍA Y VALORES ESTÁTICOS DE LOS PERFILES EN CADA PUNTO DE LOS MISMOS EN FUNCIÓN DEL ÁNGULO DE CORTE (θ)
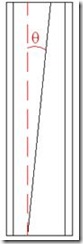
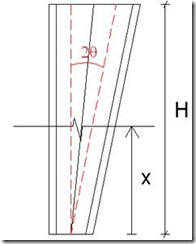
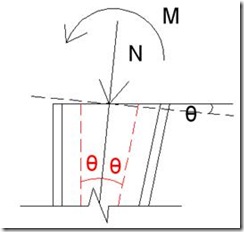
3.1) Diseño del perfil de geometría variable. Ángulo de corte (θ)
Conocidas las leyes de esfuerzos internos de las diferentes barras de la estructura, el objetivo ahora es encontrar un perfil de sección variable que satisfaga en cada punto las condiciones de tensión a las que debe estar sometida cada barra.
Se ha propuesto un perfil en doble “T”, en concreto el modelo IPE. Se trata entonces de cortar el perfil longitudinalmente con un ángulo θ, para posteriormente girar 180º una mitad del perfil y soldarla a la otra mitad, obteniendo así un perfil de sección creciente. Para mayor claridad se muestra a continuación el proceso de elaboración:
Partimos del perfil IPE.
A continuación cortamos la barra longitudinalmente con un ángulo θ.
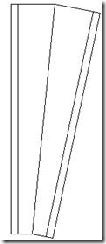 Separamos las dos mitades de barra y giramos una de ellas 180º para a continuación soldarlas
Separamos las dos mitades de barra y giramos una de ellas 180º para a continuación soldarlas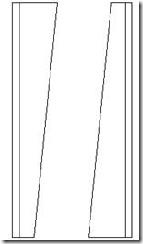 .
.
→
Finalmente enrasamos los extremos y obtenemos un perfil con sección e inercia variables.
EXTREMO SUPERIOR EXTREMO INFERIOR
ALZADO
La disposición de los perfiles del pórtico se realizará de manera que el eje fuerte de los mismos (eje x) se someta a las cargas del plano de la estructura que se contemplaron en el apartado 2.2):
3.2) Valores estáticos de alma y de alas en el plano de la estructura
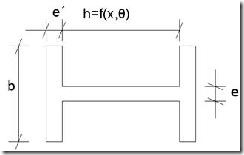
Los valores estáticos de la sección del perfil, irán variando con la longitud de la barra, pero para estudiarlos podemos separar las alas, las cuales serán de dimensiones constantes, y el alma, que en este caso será el único elemento que varíe.
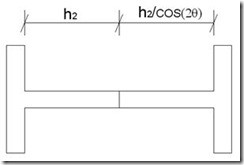
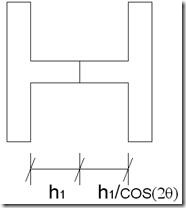
Mediante razones trigonométricas se obtiene la longitud variable del alma (h) en función de la longitud de la barra y del ángulo de corte:
* NOTA: cos(2θ) → 1
ÁREA DE UN ALA
MOMENTO DE INERCIA DE UN ALA RESPECTO DEL EJE X DE LA SECCIÓN
ÁREA DEL ALMA
MOMENTO DE INERCIA DEL ALMA RESPECTO DEL EJE X DE LA SECCIÓN
3.3) Ecuaciones finales de los valores estáticos del perfil. Coeficiente de corrección de valores
Para obtener los valores de área y momentos de inercia totales solo tendremos que sumar los valores parciales correspondientes al alma y a las alas:
También podemos ya conocer el módulo resistente de la sección respecto del eje x:
Estos valores estáticos obtenidos no son del todo ciertos, ya que en la construcción de los perfiles de acero reales, la unión del alma y el ala no es en ángulo recto sino que hay un chaflán que refuerza la unión. Tras realizar algunas comprobaciones con el prontuario de perfiles de la EA-95, he considerado que si se incrementan los resultados obtenidos anteriormente multiplicando por un coeficiente de corrección, obtenemos unos valores bastante aproximados a los reales. Pero aún así son algo menores, por lo que nos quedamos del lado de la seguridad (ver archivo Excel: “Ajuste geometría aproximada de perfiles”). Por tanto:
COEF. CORRECCIÓN PARA ÁREA: 1.02 (es decir, incrementamos el área en un 2%)
COEF. CORRECCIÓN PARA MOMENTO DE INERCIA Y MÓDULO RESISTENTE: 1.03 (es decir, incrementamos el valor en un 3%)
4) APLICACIÓN INFORMÁTICA PARA EL CÁLCULO DE PÓRTICOS TRIARTICULADOS CON PERFILES DE SECCIÓN E INERCIA VARIABLES
4.1) Filosofía y funcionamiento de la hoja de cálculo
Con los resultados obtenidos hasta el momento ya es posible obtener el perfil de inercia variable óptimo para unas condiciones dadas, hipótesis de carga (q, p, s, v1, v2) dimensiones del pórtico (L, H, F), perfil (número de IPE) y ángulo de corte (θ).
Una vez conocidas las cargas obtendríamos las reacciones, a continuación podríamos conocer las leyes de esfuerzos internos, y a partir de aquí, introduciendo un perfil concreto y un ángulo de corte, podríamos despejar las tensiones en cada sección a lo largo de la barra, ya que:
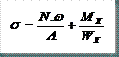 * NOTA: Despreciamos la tensión por cortante
* NOTA: Despreciamos la tensión por cortante
σ = Tensión en una sección de la barra
N = Esfuerzo axial actuante sobre una sección
A = Área de la sección del perfil en un punto a lo largo de la barra
ω = Coeficiente de pandeo de la barra
Mx = Momento flector actuante sobre una sección
Wx = Módulo resistente de la sección del perfil en un punto a lo largo de la barra
Hay que destacar que al considerar los valores de área y módulo resistente calculados en el apartado 3.3), estamos cometiendo un error. Y este se debe a que los esfuerzos axiales y por flector calculados en 2.4) inciden sobre secciones horizontales en el caso de los soportes, e inclinadas un ángulo α respecto a la vertical en el caso de los semidinteles. Sin embargo, al introducir perfiles de sección variable, la directriz del perfil ya no es la misma sino que se desvía un ángulo igual al de corte (θ) respecto a la directriz de un perfil de sección constante:
No obstante, he comprobado que los ángulos de corte cuando trabajamos con dimensiones normales e hipótesis de carga habituales suelen ser pequeños en pórticos triarticulados y biarticulados (de 0º a 4º) y más aún en pórticos biempotrados (de 0º a 2º). Por tanto consideraré que este error cometido es prácticamente despreciable y emplearé las ecuaciones antes calculadas.
Otra cuestión no sencilla es la estimación del coeficiente de pandeo (ω), ya que el coeficiente de esbeltez (β) y el radio de giro de la sección son variables, y esto dará lugar a una esbeltez mecánica (λ) variable con la que obtendremos un ω diferente en cada sección a lo largo de la barra. En esta ocasión tomaré un ω = 3 constante para toda la barra, que suele ser un valor usual para este caso. La mayor profundización en este tema requeriría otro trabajo paralelo, el cual intentaré llevar a cabo más adelante.
Por tanto, para un ángulo de corte dado, podemos obtener el área y el módulo resistente del perfil variable en función de la longitud de la barra (x). Y junto con las leyes de esfuerzos axiales y flectores en función de x, podríamos conocer la tensión en cualquier sección del perfil. Este proceso es sencillo de realizar, pero muy laborioso de cálculo, además de requerir sucesivas iteraciones con distintos ángulos de corte hasta encontrar el óptimo. Por ello diseñado una aplicación informática en una hoja de cálculo (ver archivo adjunto de Excel: CÁLCULO PÓRTICOS INERCIA VARIABLE), que permite realizar este proceso rápidamente y ajustar el ángulo de corte necesario para obtener las tensiones deseadas en cualquier sección de la barra. No obstante, este programa sólo permite el cálculo de pórticos triarticulados, aunque más adelante mostraré una propuesta para transferir los resultados a pórticos biarticulados y biempotrados.
4.2) Introducción de dimensiones del pórtico y de las cargas actuantes ponderadas. Obtención de reacciones. Obtención de leyes de esfuerzos internos
En primer lugar tenemos una serie de columnas en las que debemos introducir las dimensiones del pórtico (L, H, F) que deseamos calcular, así como las cargas ponderadas linealmente distribuidas sobre las barras (q, p, s, v1, v2) de la hipótesis previamente evaluada. Por lo general las columnas con datos en negro son las de entrada de datos, y las de colores, son las de salidas. No hay que olvidar que las cargas deben ser introducidas con su signo correspondiente según el convenio tomado en el apartado 2.2).
Instantáneamente, el programa nos dará en cuatro columnas las correspondientes reacciones en los apoyos de la estructura (YA, XA, YB, XB), también siguiendo el convenio de signos acordado.
También obtendremos los esfuerzos internos (N, M, T) para los dos soportes y los dos semidinteles, pero previamente debemos introducir en la columna “longitud barra” los valores he intervalos de “x” de las secciones en las que queremos conocer los esfuerzos (en el caso de los dinteles, metemos valores en proyección horizontal (semiluz)). Por defecto yo he considerado intervalos de 10 cm, es decir, tendré información de los esfuerzos generados en secciones de 10 en 10 cm a lo largo de la barra. Además de esto, el programa permite ver los diagramas de esfuerzos para cada barra.
4.3) Selección de los valores de esfuerzos más desfavorables
Conocidos los esfuerzos para los valores de “x” que el usuario haya deseado, se deberán elegir los valores de los mismos más desfavorables para posteriormente utilizarlos en el cálculo de las tensiones y así dimensionar las barras suponiendo que trabajen en la hipótesis más desfavorable. Para hacer esto, se tomarán los valores absolutos mayores de esfuerzos para cada “x” de entre los dos soportes, e igualmente para los dos semidinteles, y se pondrán en las columnas llamadas “COMBINACIÓN”.
4.4) Introducción del perfil de prueba y del ángulo de corte (θ). Introducción de valores geométricos invariables del perfil
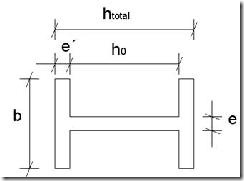
Estamos en el último módulo del programa, en el que seleccionamos un perfil determinado introduciendo el modelo en la columna “IPE”, así como las dimensiones invariables del mismo (longitud ala (b), espesor ala (e´), espesor alma (e)). Como salidas obtendremos la dimensión variable del perfil (longitud alma (h)), así como los valores de área y módulo resistente del perfil para cada sección a lo largo de la barra. Los resultados serán dados por intervalos iguales a los fijados en el cálculo de esfuerzos (en este caso cada 10 cm).
Finalmente introducimos el ángulo de corte deseado y automáticamente el programa nos dice las tensiones a lo largo del perfil (también en intervalos de 10 cm).
4.5) Obtención de tensiones. Ajuste de alma mínima de soldadura. Concentración de tensiones
Si vemos que con el perfil y ángulo de corte elegidos la tensión en algún punto supera los 2600 Kp/cm2 (tensión de agotamiento del acero) entonces debemos volver a probar otro perfil o ángulo que den resultados por debajo de dicho valor.
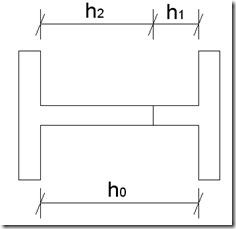
Hay que tener en cuenta que no podemos aumentar el ángulo de corte hasta su valor máximo posible de manera que h2 = h0 y h1 = 0, ya que los extremos de las barras deben de tener una longitud de alma mínima para poder soldarse correctamente a otra barra o a una placa de asiento, y además debemos evitar el efecto de concentración de tensiones. Como criterio he tomado que:
- h1 ≥ 0.2h0 (Según el libro de R. Argüelles Álvarez)
- h1 ≥ 3.5 cm
Tomaremos el mayor de ellos, es decir, si el 20% de h0 es menor que 3.5 cm, nos quedaremos con 3.5 cm, por que así, como mínimo tendremos 2h1 = 7 cm de longitud de alma en el extremo reducido, aproximadamente el alma de un IPE 80; y considero que una sección de menor alma que esta es difícil de manipular en obra. Por el contrario si el 20% de h0 es mayor que 3.5 cm, entonces tomaremos como valor mínimo este 0.2h0, en este caso para evitar que el alma del extremo reducido sea menor que la cuarta parte del alma del extremo aumentado. Con esto de alguna forma se evitará que el efecto de concentración de tensiones sea excesivo.
4.6) Resultados obtenidos para hipótesis de carga habituales. Porcentajes de ahorro de acero
Finalmente, y con las consideraciones necesarias, podríamos calcular el perfil de inercia variable que más se ajuste a nuestras necesidades utilizando esta simple hoja de cálculo. No obstante he querido dar un paso más, y utilizando este programa, he analizado diversos casos de cargas y dimensiones de pórticos habituales, llegando a estimar el porcentaje de acero que ahorramos si cambiamos los perfiles de sección constante por perfiles de sección variable. Como muestra voy a citar un caso concreto:
DIMENSONES DEL PÓRTICO
L = 10m
H = 5m
F = 2m
HIPÓTESIS DE CARGA
q = 400 Kp/m
p = 220 Kp/m
s = 110 Kp/m
v1 = 5 Kp/m
v2 = -29 Kp/m
Introduciendo estos datos en el programa obtengo finalmente que el perfil de sección constante (tomando ángulo corte θ = 0) necesario para satisfacer la condición de tensión en cada sección es un IPE 220, tanto para los soportes como para los semidinteles.
Por el contrario si opto por elegir perfiles de inercia variable, llego al resultado siguiente:
- Perfil para soportes: IPE 180 (θ = 1º)
- Perfil para semidinteles: IPE 180 (θ = -1º)
* NOTA: Seguir convenio signos para θ del apartado 3.1)
A la vista de los resultados puedo calcular el acero que nos ahorramos por pórtico:
Área IPE 220 = 33.4 cm2
Área IPE 180 = 23.9 cm2
Porcentaje de ahorro de acero = ![]() %
%
Vemos que ahorramos una cantidad importante de acero.
5) ADAPTACIÓN DEL ÁNGULO DE CORTE (θ) DE PÓRTICOS TRIARTICULADOS A PÓRTICOS BIARTICULADOS Y BIEMPOTRADOS
5.1) Descripción de los pórticos biarticulados y biempotrados
Una vez realizado el estudio del pórtico triarticulado, he realizado un intento de trasladar los resultados a los pórticos biarticulados y biempotrados, los cuales son más usados en la práctica constructiva debido a que los perfiles resultantes del análisis suelen ser menores. Para comenzar, es necesario describir con detalle las nuevas estructuras que se pretenden analizar.
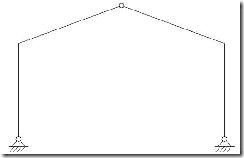
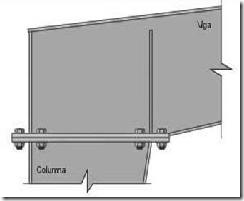
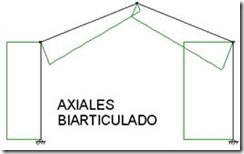
El pórtico biarticulado es semejante al triarticulado en el sistema de apoyo de soportes, pero sin embargo, la unión entre semidinteles es un nudo rígido, y no una articulación como en el caso anterior. Esta estructura es hiperestática de grado 1, ya que aparece una reacción adicional de momento en la unión de dinteles que era nulo en la estructura isostática (ver Figura 7).
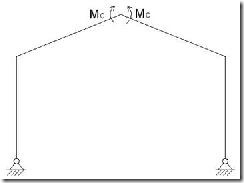 Este nudo rígido se consigue materializar en la práctica al igual que las uniones soporte-semidintel, bien sea con placas atornilladas o mediante soldadura (ver Figura 8).
Este nudo rígido se consigue materializar en la práctica al igual que las uniones soporte-semidintel, bien sea con placas atornilladas o mediante soldadura (ver Figura 8).
Figura 7. Pórtico biarticulado
Figura 8. Unión rígida entre semidinteles
Por otra parte, el pórtico biempotrado difiere más de los anteriores en cuanto a nudos se refiere. Este no tiene ninguna articulación, sino que consta de nudos rígidos en todas las uniones de barras y los apoyos de pilares se consideran empotramientos perfectos, es decir, el giro del nudo no esta permitido. Por ello ahora tenemos 3 reacciones adicionales, el momento en el nudo superior y los momentos de reacción en los apoyos (ver Figura 9).
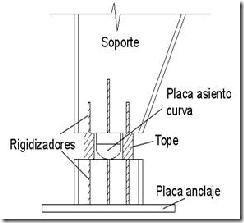
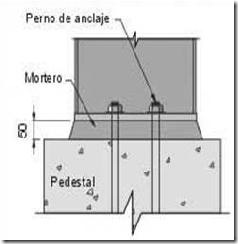
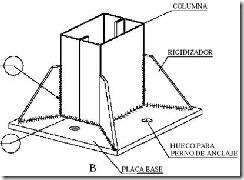
 Los empotramientos en la base de las columnas se consiguen poniendo rigidizadores y atornillando fuertemente la placa de asiento y anclaje a cimentación (ver Figura 10).
Los empotramientos en la base de las columnas se consiguen poniendo rigidizadores y atornillando fuertemente la placa de asiento y anclaje a cimentación (ver Figura 10).
Figura 9. Pórtico biempotrado
Figura 10. Apoyo rígido de columna
5.2) Transferencia de resultados del pórtico triarticulado al biarticulado
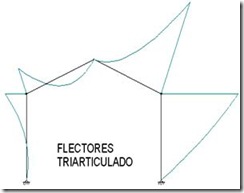
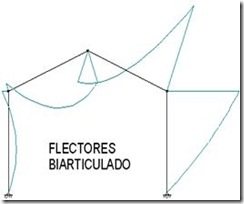
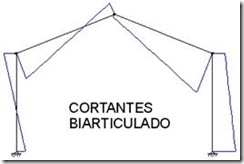
Inicialmente intente hacer este paso de transferencia a través de los esfuerzos, es decir, una vez conocidas las leyes de esfuerzos para el pórtico isostático, las equivalentes para el biarticulado estarían relacionadas con las anteriores según una ecuación algebraica. Pensé en esto porque al ver los diagramas de axiales, flectores y cortantes se puede apreciar como estos sufren un desplazamiento en horizontal o vertical respecto a la barra, y en el caso de los flectores en soportes, también se dan giros:
La dificultad reside en obtener las ecuaciones que rigen dichos desplazamientos. Por ello, finalmente decidí intentar la transferencia interpolando el ángulo de corte (θ), de manera que el θ para el pórtico biarticulado sea una función del θ del pórtico triarticulado. También se interpolaría el perfil IPE necesario de una a otra estructura. Para conseguir esto, no he tenido más remedio que analizar varios casos diferentes, variando las dimensiones del pórtico y los valores de las cargas. Aunque gracias a la hoja de cálculo he podido hacerlo más o menos rápido.
Después de varias pruebas utilizando el programa CYPE (METAL) para obtener los esfuerzos del pórtico hiperestático, he llegado a la conclusión de que los perfiles IPE y los ángulos de corte necesarios para la estructura biarticulada son los mismos que en la triarticulada, sólo que en el primer caso los flectores máximos serán menores por haber un mejor reparto de cargas en los dinteles (ya que no hay articulación entre ambos y la continuidad de esfuerzos contribuye a un reparto más homogéneo en las barras). Los axiales y cortantes son muy similares.
Existe sólo un caso concreto en el que los ángulos de corte varían, y este ocurre cuando la carga de viento es débil y/o la altura grande respecto a la luz. En este caso los dinteles del pórtico biarticulado sufren flectores parecidos en sus dos extremos por lo que el ángulo de corte (θ) tiende a hacerse nulo, para reforzar la unión dintel-dintel donde los flectores ahora son más grandes que en los demás casos; sin embargo, en el pórtico triarticulado el flector en este punto sigue anulándose al existir una articulación, por lo que θ tiende a ser mayor (-2º,-3º).
Entonces la solución del perfil variable será del tipo:
SOPORTE → IPE (…), +θº
θ suele estar comprendido entre 0º y +4º.
- θ ≤ +1º. Se da cuando las luces son pequeñas respecto a la altura y la carga de viento es pequeña.
- +1º ≤ θ ≤ +2º. Se da en los casos más habituales, cuando las luces son del orden del doble de la altura, pero de no muy grandes dimensiones, y las cargas son las usuales en naves industriales.
- +2º ≤ θ ≤ +3º. Cuando la luz es pequeña respecto a la altura y la carga de viento es considerable.
- +3º ≤ θ ≤ +4º. Para luces grandes en relación a las alturas.
SEMIDINTEL → IPE (…), -θº
θ suele estar comprendido entre 0º y -3º.
- 0º ≥ θ ≥ -1º. Ocurre en casos en los que la altura es grande respecto a la luz y la carga de viento es débil.
- -1º ≥ θ ≥ -2º. Para casos habituales, cuando las luces son del orden del doble de la altura, pero de no muy grandes dimensiones, y las cargas son las usuales en naves industriales.
- -2º ≥ θ ≥-3º. Cuando las luces son grandes respecto a la altura, o cuando el viento es grande.
Hay que decir que estos valores son sólo orientativos, ya que los he obtenido probando varios modelos de carga y dimensiones diferentes hasta llegar a intuir la tendencia del ángulo de corte en cada caso. Por ello, esto no quiere decir que no haya casos particulares que no cumplan las reglas propuestas, ya que no lo puedo asegurar.
Después de estas elucubraciones, he intentado estimar el ahorro de acero obtenido usando barras de sección variable para este tipo de estructuras. Para ello he calculado los esfuerzos con el programa CYPE (para ahorrarme el método de rigidez) usando las mismas cargas del ejemplo del pórtico isostático, y luego las he introducido en la hoja de cálculo para obtener los resultados de perfil variable y obtener el ahorro de IPE respecto a la opción de sección constante. Por tanto:
DIMENSONES DEL PÓRTICO
L = 10m
H = 5m
F = 2m
HIPÓTESIS DE CARGA
q = 400 Kp/m
p = 220 Kp/m
s = 110 Kp/m
v1 = 5 Kp/m
v2 = -29 Kp/m
Los resultados obtenidos son similares a los del pórtico triarticulado. Reducimos de un IPE 220 a un IPE 180, por lo que el porcentaje de acero ahorrado es del 28%.
5.3) Transferencia de resultados del pórtico triarticulado al biempotrado
Ahora se trata de realizar la misma operación anterior, pero para estimar los perfiles de inercia variable necesarios en la estructura biempotrada. Después de comprobar diversos casos diferentes de dimensión y carga he llegado a la conclusión general de que los perfiles necesarios para este caso son semejantes a los del pórtico triarticulado y biarticulado, con la única salvedad de que el ángulo de corte (θ) es diferente:
SOPORTE → IPE (…), +θº
Esta regla se cumple habitualmente, excepto en el caso de alturas grandes respecto a la luz y carga de viento fuerte, donde θ tiende a ser nulo para reforzar el perfil ante un aumento del momento flector en la base del pilar. Este efecto es consecuencia del empotramiento en la base.
SEMIDINTEL → IPE (…), -θº
Aquí la excepción se produce cuando las alturas son grandes respecto a la luz y la carga de viento es débil. θ tiende a 0 para reforzar el perfil ante un aumento del flector en la unión de dinteles. Esta excepción es conocida, ya que ocurre también en el pórtico biarticulado.
Ahora veamos el porcentaje de ahorro de acero que obtenemos diseñando esta estructura con los perfiles de sección variable, respecto al diseño con sección constante. Utilizando los datos de los casos anteriores:
DIMENSONES DEL PÓRTICO
L = 10m
H = 5m
F = 2m
HIPÓTESIS DE CARGA
q = 400 Kp/m
p = 220 Kp/m
s = 110 Kp/m
v1 = 5 Kp/m
v2 = -29 Kp/m
Después de los cálculos se obtiene que para θ = 0 (sección constante) el perfil necesario es un IPE 200, tanto para soportes como para dinteles. En cambio, si usamos perfil de sección variable tenemos:
- Perfil para soportes: IPE 180 (θ = 0.5º)
- Perfil para semidinteles: IPE 180 (θ = -0.5º)
Área IPE 200 = 28.5 cm2
Área IPE 180 = 23.9 cm2
Porcentaje de ahorro de acero = 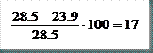 %
%
Vemos en este caso que el ahorro de acero es menor que si utilizamos apoyos de soportes articulados (28%).
5.4) Conclusión y problemas del método. Alternativas
La verdad es que este método propuesto para transferir los resultados de unas estructuras a otras es sólo aproximado y no siempre preciso, aunque se suele cumplir para los casos más normales.
Otra solución para obtener los perfiles de inercia variable óptimos para los pórticos hiperestáticos podría ser la siguiente:
1) Introducir en un programa de cálculo de estructuras (por ejemplo CYPE) el pórtico hiperestático que deseamos calcular, pero discretizando las barras a intervalos más o menos pequeños dependiendo de las dimensiones totales del pórtico. Así cada barra estará compuesta de uniones rígidas de muchas barras pequeñas (sub-barras) y nos será más fácil conocer los esfuerzos en puntos intermedios del perfil.
2) Después de esto, dimensionamos la estructura con el perfil necesario en cada sub-barra, obteniendo como resultado sub-barras con perfiles IPE diferentes en cada tramo de discretización, lo que da lugar a una barra total de inercia variable. No obstante esta barra no es la del caso que se estudia en este trabajo, ya que aquí obtenemos el resultado como si soldáramos sucesivamente perfiles IPE diferentes hasta componer la barra, lo cual no se asemeja al método propuesto del ángulo de corte. De todas maneras, este artilugio si que nos puede ser útil, ya que el objetivo es conocer los esfuerzos (Axial y Flector) en extremos de cada sub-barra, para luego llevarlos a la hoja de cálculo en Excel y obtener el perfil IPE y el ángulo de corte (θ). Por tanto, yo creo que las leyes de esfuerzos obtenidas para la barra variable compuesta de sub-barras, y la barra variable formada por corte, giro y soldadura deben ser parecidas; y por ello podemos aplicarlas en la hoja Excel para obtener nuestro perfil de sección variable buscado.
Voy a ilustrar un poco este método:
Primero diseñamos en CYPE la estructura discretizada. En este caso es el pórtico biarticulado, y las sub-barras que he elegido son de 25 cm de largo.
Calculamos la estructura y comprobamos las barras sucesivamente hasta obtener los perfiles IPE necesarios para cada sub-barra, consiguiendo finalmente soportes y semidinteles de inercia variable.
FRONTAL PERSPECTIVA
Obtenemos las leyes de esfuerzos de la estructura.
Finalmente conocidos los esfuerzos, tomamos los valores discretos de axial y flector (el cortante lo obviamos por generar tensiones triviales respecto a las otras tensiones), y los llevamos a la hoja de Excel “CÁLCULO PÓRTICOS INERCIA VARIABLE”. De esta manera obtendremos los perfiles óptimos para este pórtico.
6) DISCUSIÓN DE RESULTADOS. VENTAJAS E INCONVENIETES DE CADA TIPO DE PÓRTICO. RELACIÓN DEL COSTE DE ESTRUCTURA CON EL COSTE DE CIMENTACIÓN
Para finalizar este trabajo, realizaré una discusión de los resultados obtenidos con el fin de ver que ventajas e inconvenientes tiene cada modelo estructural, y cuando es preferible utilizar perfiles de inercia variable en sustitución a los de inercia constante.
A) PÓRTICO TRIARTICULADO
Este tipo estructural es sinceramente no recomendable, ya que tiene las mismas ventajas que el pórtico biarticulado, pero al tener una unión dintel-dintel articulada, los momentos flectores máximos (los cuales se producen en la unión dintel-soporte) son superiores, y por tanto suelen resultar muchas veces perfiles mayores. Por otro lado la materialización del nudo articulado entre dinteles puede ser más difícil de ejecutar y por tanto más caro.
B) PÓRTICO BIARTICULADO VS PÓRTICO BIEMPOTRADO
Como ventaja general del pórtico biarticulado, podemos decir que al tener rótulas (articulaciones) en la base de soportes, no se transmiten momentos flectores a cimentación, lo cual conllevará menor gasto económico en este apartado. En cambio, el pórtico biempotrado si que transmite flectores a cimentación, y si estos son muy grandes la cimentación será cara.
Otro aspecto a tener en cuenta es el coste de acero de la estructura. En este caso según los resultados obtenidos tras este estudio, se llega a la conclusión siguiente:
- Usando barras de sección constante: Para unas mismas dimensiones e hipótesis de carga, el p. biarticulado requiere perfiles IPE mayores que el p. biempotrado.
- Usando barras de sección variable: En este caso los perfiles necesarios en cada tipo estructural son similares.
Entones podemos finalizar diciendo que en el caso de barras de sección constante, no podemos decidir obviamente si el p. biarticulado es mejor que el biempotrado o viceversa, ya que en el primero ahorramos en cimentación y en el segundo, en acero. Por tanto habría que estudiar ya casos concretos con más detenimiento para decidirse por uno de los dos.
En cambio, si usamos barras de inercia variable, los dos pórticos necesitan normalmente el mismo perfil. Así que en este caso el p. biarticulado ganaría la partida al biempotrado, ya que tenemos un ahorro adicional en cimentación.
En cuanto al problema de decidir si usamos o no perfiles de inercia variable, la respuesta es clara. Si los costes de preparación y construcción de la barra (corte, soldadura…) son menores que el ahorro en acero, la operación será rentable. En el caso de usar este tipo de perfiles, lo recomendable entonces sería ir a pórticos biarticulados.
Francisco Javier Enríquez Santos

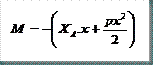
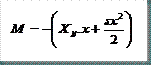
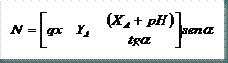
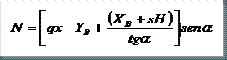
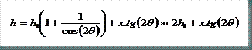
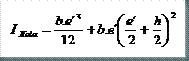
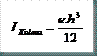
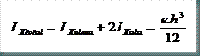
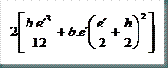
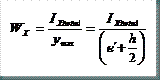

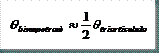
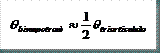
No hay comentarios.:
Publicar un comentario