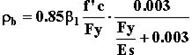| 1.1 INTRODUCCION |
| Las losas son elementos estructurales bidimensionales, en los que la tercera dimensión es pequeña comparada con las otras dos dimensiones básicas. Las cargas que actúan sobre las losas son esencialmente perpendiculares al plano principal de las mismas, por lo que su comportamiento está dominado por la flexión. |
| 1.2 TIPOS DE LOSAS |
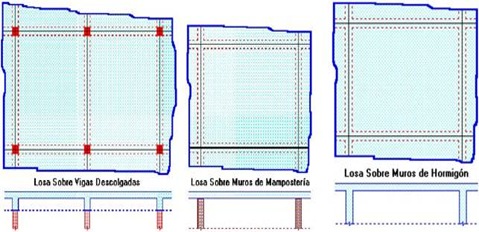
| Las losas pueden estar soportadas perimetral e interiormente por vigas monolíticas de mayor peralte, por vigas de otros materiales independientes o integradas a la losa; o soportadas por muros de concreto , muros de mampostería o muros de otro material, en cuyo caso se las llama Losas Sustentadas sobre Vigas o Losas Sustentadas sobre Muros, respectivamente. |
| Las losas pueden sustentarse directamente sobre las columnas, llamándose en este caso Losas Planas, que en su forma tradicional no son adecuadas para zonas de alto riesgo sísmico como las existentes en nuestro país, pues no disponen de capacidad resistente suficiente para incursionar dentro del rango inelástico de comportamiento de los materiales, con lo que se limita considerablemente su ductilidad. Pueden utilizarse capiteles y ábacos para mejorar la integración de las losas planas con las columnas, y para mejorar la resistencia de las losas al punzonamiento. |
| Las losas planas pueden mejorar relativamente su comportamiento ante los sismos, mediante la incorporación de vigas embebidas o vigas banda, con ductilidades apropiadas, en cuyo caso se llaman Losas Planas con Vigas Embebidas, que pueden ser útiles para edificios de hasta 4 pisos, con luces y cargas pequeñas y medianas. |
| Si la geometría de la losa y el tipo de apoyo determinan que la magnitud de los esfuerzos en dos direcciones ortogonales sean comparables, se denominan Losas Bidireccionales. Si los esfuerzos en una dirección son preponderantes sobre los esfuerzos en la dirección ortogonal, se llaman Losas Unidireccionales. |
| Cuando el concreto ocupa todo el espesor de la losa se la llama Losa Maciza, y cuando parte del volumen de la losa es ocupado por materiales más livianos o espacios vacíos se la llama Losa Alivianada o Losa Aligerada. |
| Las losas alivianadas son las más populares en nuestro país por lo que, a pesar de que los códigos de diseño prácticamente no las toman en consideración, en este documento se realizará un análisis detallado de las especificaciones que les son aplicables. Los alivianamientos se pueden conseguir mediante mampuestos aligerados de concreto (son los de mayor uso en nuestro medio), cerámica aligerada, formaletas plásticas recuperables o formaletas de madera. |
| Las dimensiones estándar y los pesos de los bloques aligerados de concreto disponibles en el mercado son: |
| a. LOSAS UNIDIRECCIONALES: |
| Las Losas Unidireccionales se comportan básicamente como vigas anchas, que se suelen diseñar tomando como referencia una franja de ancho unitario (un metro de ancho). Existen consideraciones adicionales que serán estudiadas en su momento. |
| Cuando las losas rectangulares se apoyan en dos extremos opuestos, y carecen de apoyo en los otros dos bordes restantes, trabajan y se diseñan como losas unidireccionales. |
| Cuando la losa rectangular se apoya en sus cuatro lados (sobre vigas o sobre muros), y la relación largo / ancho es mayor o igual a 2, la losa trabaja fundamentalmente en la dirección más corta, y se la suele diseñar unidireccionalmente, aunque se debe proveer un mínimo de armado en la dirección ortogonal (dirección larga), particularmente en la zona cercana a los apoyos, donde siempre se desarrollan momentos flectores negativos importantes (tracción en las fibras superiores). Los |
| momentos positivos en la dirección larga son generalmente pequeños, pero también deben ser tomados en consideración. |
| b. LOSAS BIDIRECCIONALES: |
| Cuando las losas se sustentan en dos direcciones ortogonales, se desarrollan esfuerzos y deformaciones en ambas direcciones, recibiendo el nombre de Losas Bidireccionales. |
| La ecuación general que describe el comportamiento de las losas bidireccionales macizas, de espesor constante, es conocida como la Ecuación de Lagrange o Ecuación de Placas, que se presenta a continuación: |
| Donde: |
| w : ordenada de la elástica de deformación de la placa en un punto de coordenadas (x, y) D : rigidez a la flexión de la placa, análoga al producto E . I en vigas E : módulo de elasticidad longitudinal del concreto h : espesor de la placa m : coeficiente de Poisson del concreto (su valor está comprendido entre 0.15 y 0.20) |
| La ecuación de Lagrange utiliza como fundamento la Ley de Deformación Plana de Kirchhoff que establece que una placa plana delgada, sometida a cargas perpendiculares a su plano principal, se deformará de modo que todos los puntos materiales que pertenecen a una recta normal a la superficie sin deformarse permanecerán dentro de la correspondiente recta normal a la superficie deformada (la versión simplificada para vigas diría que las secciones transversales planas antes de la deformación permanecen planas después de la deformación). |
| Las solicitaciones unitarias internas que se desarrollan en las placas quedan definidas por las siguientes expresiones. |
| Donde: mx : momento flector alrededor del eje x, por unidad de ancho de losa my : momento flector alrededor del eje y, por unidad de ancho de losa mxy : momento torsor, por unidad de ancho de losa vx : esfuerzo cortante en la dirección x, por unidad de ancho de losa vy : esfuerzo cortante en la dirección y, por unidad de ancho de losa |
| Es importante notar que las deformaciones producidas por flexión en una de las direcciones generan esfuerzos flexionantes en la dirección perpendicular debido al efecto de Poisson. También debe tomarse en consideración de que simultáneamente a la flexión en las dos direcciones, aparecen momentos torsionantes que actúan sobre la losa. |
| Las dos primeras ecuaciones son análogas a la Ecuación General de la Flexión en Vigas, pero se incluye la deformación provocada por los momentos flexionantes transversales. |
| Las solicitaciones de diseño para las losas bidireccionales dependen de las cargas y las condiciones de apoyo. Existen tablas de diseño de losas para las cargas y las condiciones de apoyo (o de carencia de apoyo) más frecuentes (empotramiento o continuidad total; apoyo fijo con posibilidad de rotación; borde libre o voladizo), y en casos de geometrías y cargas excepcionales se pueden utilizar los métodos de las Diferencias Finitas o de los Elementos Finitos. |
| 1. 3 ESPECIFICACIONES CODIFICADAS PARA LOSAS |
| a. DEFLEXIONES MAXIMAS EN LOSAS: |
| El Reglamento Nacional de Construcciones y el ACI definen deflexiones máximas calculadas para losas macizas y nervadas que varían desde Ln/180 hasta Ln/480, dependiendo del uso de la losa. |
| Máximas Deflexiones Permisibles Calculadas en Losas |
| Para el caso de losas rectangulares apoyadas sobre vigas de mayor peralte cuya relación lado largo / lado corto sea menor que 2, el cálculo de las deflexiones se realiza con tres ecuaciones propuestas por los códigos. |
| La ecuación básica define una altura mínima genérica para la losa: |
| Donde: |
| h: peralte o espesor de la losa maciza o altura de inercia equivalente en la losa nervada Ln : claro libre en la dirección larga del panel, medido de cara a cara de las columnas en losas sin vigas, y de cara a cara de las vigas en losas sustentadas sobre vigas Fy : esfuerzo de fluencia del acero en Kg/cm2 a m : promedio de los valores de a para las cuatro vigas en los bordes del panel, donde |
| a : relación entre E . I de la sección de la viga y E . I del ancho de la losa limitada lateralmente por las líneas de centro de los paneles adyacentes a cada lado de la viga (donde las hubiera) b : relación de forma del panel = panel largo libre / panel corto libre b s : relación entre la longitud de los bordes continuos del panel y el perímetro del panel (1 para un panel interior, ½ para un panel esquinero) |
| Los resultados de la ecuación anterior no deben ser menores que la siguiente expresión: |
| Así mismo, el valor obtenido con la ecuación básica no necesita ser mayor que la siguiente expresión: |
| Además de las expresiones anteriores, el Reglamento Nacional de Construcciones establece que la altura de las losas no debe ser menor que los siguientes valores: Losas sin vigas o ábacos ................................................. 12 cm Losas sin vigas pero con ábacos que cubran al menos un sexto de la luz centro a centro y se proyecten por debajo de la losa al menos h/4 ........................................ 10 cm Losas que tengan vigas en los cuatro bordes, con un |
| valor de a m por lo menos igual a 2.0 ............................... 9 cm El Reglamento Nacional de Construcciones y el ACI también especifican un peralte mínimo de las losas armadas en una sola dirección para limitar las deflexiones a valores razonables, cuando no se calculan deflexiones. La siguiente tabla puede ser usada también para losas bidireccionales sobre vigas de mayor peralte cuya relación lado largo / lado corto sea mayor que 2 (trabajan fundamentalmente en la dirección corta), arrojando resultados conservadores. |
| Altura Mínima de Vigas o Losas en una Dirección Cuando no se Calculan Deflexiones |
| Donde: |
| Ln: claro libre en la dirección de trabajo de la losa, medido de cara interna a cara interna de los elementos que sustentan a la losa |
| ING. CIVIL-UNS |
| b. ARMADURA MINIMA: |
| En losas de espesor constante (losas macizas), cuando se utilice acero de refuerzo con esfuerzo de fluencia Fy = 2800 Kg/cm2 o Fy =3500 Kg/cm2, la cuantía de armado mínimo para resistir la retracción de fraguado y los cambios de temperatura ρ mín será de 0.0020, en dos direcciones ortogonales. Esta armadura no debe colocarse con separaciones superiores a 5 veces el espesor de la losa ni 45 cm. |
| En losas de espesor constante, cuando se utilice acero de refuerzo con Fy = 4200 Kg/cm2, la cuantía mínima para resistir cambios temperatura y retracción de fraguado ρ mín será de 0.0018, y los espaciamientos serán similares al punto anterior. |
| En losas nervadas, la cuantía mínima de flexión ρ mín se calculará mediante la siguiente expresión: |
| El armado en losas nervadas se calculará tomando como ancho de la franja de concreto el ancho de los nervios. |
| En la loseta de compresión de las losas nervadas deberá proveerse de acero de refuerzo para resistir la retracción de fraguado y los cambios de temperatura, de un modo similar a las losas macizas de espesor constante. |
| La diferencia entre las especificaciones para losas nervadas y para losas macizas se produce por que los nervios de las losas nervadas se comportan fundamentalmente como una malla espacial de vigas, y la loseta de compresión se comporta como una combinación de placa y membrana. |
| c. ARMADURA MAXIMA: |
| Con el objeto de asegurar una ductilidad mínima, no se podrá proporcionar más armadura a una losa que el 75% de la cuantía balanceada cuando no resiste sismo, y que el 50% de la cuantía balanceada cuando resiste sismo. |
| ρ máx = 0.75 ρ b (si las losas no resisten sismo) |
| ρ máx = 0.50 ρ b (si las losas resisten sismo) |
| La cuantía balanceada está definida por: |
| Donde: |
| ρ b: cuantía balanceada f’c: resistencia característica a la rotura del concreto Fy: esfuerzo de fluencia del acero de refuerzo Es: módulo de elasticidad del acero |
| c. RECUBRIMIENTO MINIMO: El acero de refuerzo en losas fundidas in situ debe tener un recubrimiento mínimo de 2.5 cm. El acero de refuerzo en losas prefabricadas debe tener un recubrimiento mínimo de 1.5 cm. |
| ING. CIVIL-UNS |
| d. ABERTURAS EN LOSAS: |
| Se admiten aberturas en losas si se demuestra mediante análisis que la resistencia proporcionada es apropiada. No se requerirá de análisis especial por la presencia de una abertura en la zona central siempre que se mantenga la cantidad total de refuerzo requerido en el tablero sin la abertura. El refuerzo eliminado por la presencia de la abertura deberá colocárselo alrededor de la abertura, armando nervios o vigas embebidas de borde. |
| EJEMPLO 1.1: |
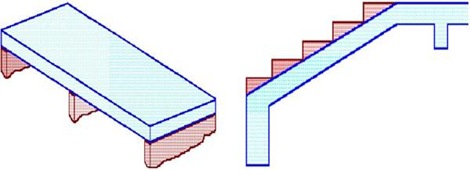
| Diseñar la siguiente escalera construida con concreto de resistencia característica f’c = 210 Kg/cm2 y acero con esfuerzo de fluencia Fy = 4200 Kg/cm2: |
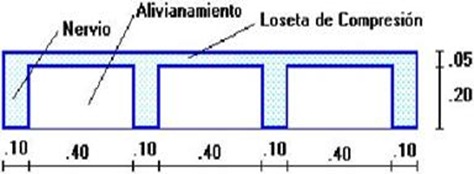
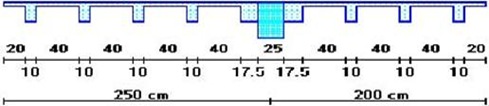
| Se utilizará tentativamente una losa alivianada armada en una dirección, con un espesor de 25 cm, con loseta de compresión de 5 cm de espesor, con nervios de 10 cm de ancho cada 50 cm. Los nervios de distribución transversales se colocarán cada metro de distancia. |
| Control de Deflexión: |
| hmín = Ln / 18.5 = (400 cm - 30 cm) /18.5 = 20 cm h = 25 cm > hmín (O.K.) |
| Determinación de las Cargas de Diseño: Peso loseta de compresión = 1.60 x 1.00 x 0.05 x 2400 = 192 Kg/m Peso nervios longitudinales = 4 x 0.10 x 0.20 x 2400 = 192 Kg/m |
| ING. CIVIL-UNS |
| Peso de nervios transversales = 0.10 x 0.20 x 1.60 x 2400 = 77 Kg/m Alivianamientos = 15 bloques x 12 Kg/bloque = 180 Kg/m |
| Peso Propio = 641 Kg/m |
| Peso relleno gradas = 1.60 x 1.00 x 0.09 x 2000 = 288 Kg/m Enlucido y masillado = 1.60 x 1.00 x 0.04 x 2200 = 141 Kg/m Recubrimiento de piso = 1.60 x 1.00 x 0.02 x 2200 = 71 Kg/m Pasamanos = 50 Kg/m |
| Carga Permanente = 1191 Kg/m Carga Viva = 1.60 x 500 = 800 Kg/m Carga Ultima de Diseño U = 1.4 D + 1.7 L = 1.4 (1191) + 1.7 (800) = 3027 Kg/m |
| Modelo Estructural de la Escalera y Reacciones de Apoyo: |
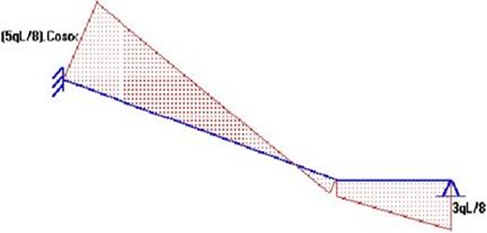
| Diagrama de Momentos Flectores: |
| Diagrama de Fuerzas Cortantes: |
| Determinación de Momentos Flectores Ultimos de Diseño: |
| El momento flector negativo se calcula en la cara de la viga de soporte, que tiene 30 cm de base (a 15 cm del |
| Mu(-) = 4953 Kg-m = 495300 Kg-cm El momento flector positivo se calcula en el tramo: |
| Mu(+) = 3405 Kg-m = 340500 Kg-cm |
| Determinación de la Armadura Longitudinal Negativa (hierro superior): |
| Mu(-) = 495300 Kg-cm |
| Fy = 4200 Kg/cm2 |
| f'c = 210 Kg/cm2 |
| f = 0.9 (flexión) |
| b = 40 cm (cuatro nervios comprimidos) |
| d = 25 cm - 3 cm = 22 cm |
| Para calcular la sección de acero requerida en una pieza rectangular sometida a flexión se puede utilizar la |
| siguiente expresión: |
| Deberá verificarse posteriormente que no se haya sobrepasado de la fracción de cuantía de armado balanceada especificada en los códigos (75% cuando no resiste sismo y 50% cuando resiste sismo), pues la expresión detallada anteriormente presupone que el acero de refuerzo entra en fluencia. Además deberá controlarse que la cuantía de armado supere a la cuantía mínima. |
| ING. CIVIL-UNS |
| Se calcula la sección de acero para los cuatro nervios, aplicando la expresión antes señalada: |
| As = 6.53 cm2 para los cuatro nervios = 1.63 cm2 por cada nervio As = 1 Φ 16 mm por cada nervio |
| Determinación de la cuantía real de armado: |
| Verificación de la armadura máxima permisible: |
| ρ máx = 0.75 ρ b = 0.75 (0.0217) = 0.0163 ρ < ρ máx (O.K.) Verificación de la armadura mínima requerida: |
| (las losas nervadas son tratadas como vigas integradas) |
| ρ > ρ mín (O.K.) Determinación de la Armadura Longitudinal Positiva (hierro inferior): |
| b = 160 cm (ancho en la loseta de compresión) |
| As = 4.15 cm2 para los cuatro nervios As = 1.04 cm2 por cada nervio (1 Φ 12 mm por cada nervio) Determinación de la Cuantía de Armado: |
| La cuantía de armado está comprendida entre los valores mínimos y máximos permitidos. |
| Verificación del Dimensionamiento bajo Cargas de Corte: |
| La resistencia del concreto simple al cortante es: |
| ING. CIVIL-UNS |
| Se calcula el cortante solicitante: Tg(a ) = 1.30 / 2.40 a = 28.44° Vu = { (3027*4) (5/8) - 3027*(0.15+0.22) }. Cos (28.44° ) Vu = 5669 Kg. para los cuatro nervios |
| vu > vc (La sección escogida no es apropiada) |
| Se debe incrementar la sección resistente al corte, para disminuir el esfuerzo cortante, lo que se puede lograr aumentando el ancho de los nervios de 10 cm a 15 cm, lo que implicará un reajuste en la distribución de los alivianamientos. |
| Determinación de las Cargas de Diseño: |
| Peso loseta de compresión = 1.60 x 1.00 x 0.05 x 2400 = 192 Kg/m Peso nervios longitudinales = 0.15 x 0.20 x 4 x 2400 = 288 Kg/m Peso de nervios transversales = 0.10 x 0.20 x 1.60 x 2400 = 77 Kg/m Alivianamientos = 13 bloques x 12 Kg/bloque = 156 Kg/m |
| Peso Propio = 713 Kg/m |
| Peso propio de la losa = 713 Kg/m Peso relleno gradas = 1.60 x 1.00 x 0.09 x 2000 = 288 Kg/m Enlucido y masillado = 1.60 x 1.00 x 0.04 x 2200 = 141 Kg/m Recubrimiento de piso = 1.60 x 1.00 x 0.02 x 2200 = 71 Kg/m Pasamanos = 50 Kg/m |
| Carga Permanente = 1263 Kg/m Carga Viva = 1.60 x 500 = 800 Kg/m Carga Ultima de Diseño U = 1.4 D + 1.7 L = 1.4 (1263) + 1.7 (800) = 3128 Kg/m |
| ING. CIVIL-UNS |
| Determinación de los Momentos Flectores Ultimos de Diseño: Mu(-) = 3128 (4)2/8 - 3128(4)(5/8)(0.15) + 3128 (0.15)2/2 = 5118 Kg-m = 511800 Kg-cm Mu(+) = 9(3128)(4)2/128 = 3519 Kgr-m = 351900 Kgr-cm |
| Determinación de la Armadura Longitudinal: |
| As(-) = 6.77 cm2 por los cuatro nervios = 1.69 cm2 por nervio |
| As(-) = 1 Φ 16 mm en la parte superior de cada nervio |
| As(+) = 4.29 cm2 por los cuatro nervios = 1.07 cm2 por nervio |
| As = 1 Φ 12 mm en la parte inferior de cada nervio |
| ρ mín = 14 / Fy = 14 / 4200 = 0.003333 Asmín = 0.003333 (15) (22) = 1.10 cm2 por nervio |
| Asmín = 1 Φ 12 mm cada nervio Verificación del Dimensionamiento bajo Cargas de Corte: |
| Vu = { (3128*4) (5/8) - 3128*(0.15+0.22) } . Cos (28.44° ) Vu = 5859 Kg para los cuatro nervios |
| A pesar de que el análisis estructural no lo revela, pues el modelo empleado es muy simplificado, siempre existirá un pequeño momento flector negativo en la unión de la losa con la viga extrema, debido a la rigidez torsional de la viga de apoyo, que provoca algún nivel de restricción a la rotación libre. Es necesario, por consiguiente, proveer de un armado mínimo negativo a la losa para soportar tal solicitación. |
| A continuación se presenta un detalle del armado de los nervios: |
| Armadura de Temperatura y Retracción de fraguado: |
| Para absorber los esfuerzos generados en el concreto de la loseta de compresión, por concepto de cambios de temperatura y retracción de fraguado, y permitir un control eficiente de la fisuración, se puede utilizar una malla electrosoldada con esfuerzo de fluencia Fy = 2800 Kg/cm2, requiriéndose la siguiente armadura mínima en las dos direcciones: |
| ρ mín = 0.0020 |
| Asmín = ρ mín . b . d |
| Asmín = (0.0020) (100 cm) (2.5 cm) |
| Asmín = 0.50 cm2 por metro de ancho |
| El máximo espaciamiento entre alambres de la malla electrosoldada es 5 veces el espesor de la loseta o 45 cm, el que sea menor: emáx = 5 (5 cm) = 25 cm emáx < 45 cm emáx = 25 cm Se puede escoger una malla con alambres de 4 mm de diámetro espaciados cada 25 cm, que debe colocarse a |
| 1.4 TABLAS PARA EL DISEÑO DE LOSAS MACIZAS Y NERVADAS RECTANGULARES SUSTENTADAS PERIMETRALMENTE EN VIGAS: |
| Existen tablas para el diseño de losas, desarrolladas por diferentes autores, que facilitan el análisis y el diseño de las losas de geometrías y estados de carga más comunes, basadas en la mayor parte de los casos en la Teoría de Placas. |
| Se han preparado, para esta publicación, tablas para el diseño de losas sustentadas perimetralmente en vigas de mayor peralte que las losas (de este modo nos aseguramos que las deflexiones en las vigas no tienen gran influencia sobre el comportamiento de las losas), sometidas a cargas uniformemente distribuidas. El tipo de sustentación está definido por las condiciones de borde de las losas. |
| Para el modelamiento de las losas macizas se ha utilizado el Método de los Elementos Finitos basado en la Teoría de Placas, el mismo que se recomienda para analizar losas macizas de geometrías, estados de carga o condiciones de borde especiales, que no aparezcan en las tablas. Otra alternativa de análisis podría ser el uso del Método de las Diferencias Finitas. |
| Para modelar las losas nervadas se ha utilizado el Análisis Matricial de Estructuras tradicional, para estructuras conformadas por barras rectas espaciales bajo la hipótesis de que el efecto de flexión es dominante sobre las deformaciones de cortante y torsión. |
| ING. CIVIL-UNS |
| Las tablas para losas nervadas constituyen una novedad importante con respecto a otras publicaciones similares. Las deformaciones y los momentos flectores que se obtienen en el modelo de losas nervadas son generalmente mayores que los valores obtenidos en losas macizas, debido a que los momentos torsores en las placas se transforman en momentos flectores en |
| los nervios. En las tablas publicadas a continuación se presentan tres tipos genéricos de condiciones de borde: |
| El empotramiento se lo emplea para modelar la continuidad de la losa en el borde seleccionado, usualmente proporcionada por otra losa contigua de dimensiones comparables, proporcionada por un muro extremo integrado a la losa como los que se tienen en los subsuelos de las edificaciones, o proporcionada por una viga de borde de gran rigidez torsional (de gran sección y dimensiones transversales). |
| El apoyo con rotación alrededor de un eje se utiliza para modelar la presencia de una viga de borde de dimensiones normales (de peralte mayor al de la losa, pero no una viga de gran peralte ni una viga de gran sección transversal) sin losa contigua, o para modelar la presencia de un muro no integrado a la losa (usualmente muros de otro material). |
| El borde libre modela la inexistencia de una viga de borde de mayor peralte que la losa, la inexistencia de una losa contigua, o la inexistencia de un muro integrado a la losa. |
| Los 18 modelos diferentes de losas macizas que aparecen en las tablas de esta publicación, son: |
| Es importante notar que, dependiendo de las diferentes condiciones de borde, es posible que algunos modelos de losas carezcan de determinados tipos de momentos flectores (fundamentalmente los momentos flectores negativos de apoyo cuando es posible la rotación alrededor de la línea de apoyo). |
| En otros casos, es necesario definir dos momentos flectores del mismo tipo para describir su variabilidad a lo largo de la losa (dos momentos flectores positivos y dos momentos flectores negativos en los bordes sustentados, en losas con un borde en voladizo). |
| Los 18 modelos diferentes de losas nervadas que aparecen en las tablas de esta publicación, son: |
| Mediante los coeficientes adimensionales de las tablas (d , m), se pueden calcular la defexión máxima de la losa (D ), y los momentos flectores positivos y negativos máximos (M) en las dos direcciones, por unidad de ancho de la losa. |
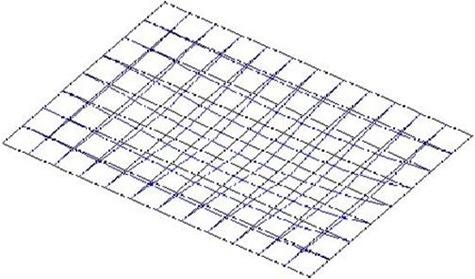
| Si se toma el tercer modelo de losa nervada, con una relación lado corto / lado largo de 0.70, la estructura idealizada sería: |
| La elástica de deformación producida por una carga uniformemente distribuida que actúe sobre toda la superficie de la losa anterior tendría la siguiente geometría: |
| Por su parte, la distribución cualitativa de los momentos flectores, en las 2 direcciones principales de la losa del ejemplo anterior, para el estado de cargas antes mencionado sería similar a la siguiente: |
| Debe observarse que, mientras la geometría (no la magnitud) del diagrama de momentos flectores en la dirección corta es muy similar al diagrama de momentos en vigas, la geometría del diagrama de momentos flectores en la dirección larga tiende a alargarse y a disminuir en su magnitud en la zona central de momentos flectores positivos. Las ordenadas de los diagramas de momentos en losas son generalmente menores a las existentes en vigas con el mismo estado de cargas, debido a la distribución de las cargas en dos direcciones. |
| Para relaciones lado corto / lado largo inferiores a 0.70 hay una tendencia clara a la aparición de 2 momentos flectores máximos positivos en la dirección larga, uno cercano a cada borde. Los momentos flectores positivos son pequeños en la zona central. Este último hecho debe ser tomado con mucho cuidado pues al utilizar cargas uniformemente distribuidas que actúen sólo en ciertos sectores de la superficie de las losas, estos momentos flectores máximos positivos se desplazan de las zonas cercanas a los bordes hacia las zonas centrales, por lo que es necesario trabajar con una envolvente de momentos flectores. Para el ejemplo anterior, la envolvente de momentos flectores en la dirección larga sería similar a la siguiente: |
| Si bien es cierto que los momentos flectores que se producen en las zonas esquineras son menores que los momentos flectores en las zonas alejadas de las esquinas, es recomendable que su armado (léase su capacidad resistente) sea similar a aquel calculado para las zonas alejadas de las esquinas, debido a la presencia de momentos torsores y deformación torsionante en las esquinas. Los momentos torsores en la losa son generalmente de un orden de magnitud inferior a los momentos flectores, por lo que usualmente no requieren de diseño especial, siempre que se emplee la recomendación anterior. En el caso de las losas nervadas, adicionalmente a la recomendación de armado esquinero, debe cuidarse de que el ancho de los nervios cerca a las esquinas sea al menos la quinta parte de la dimensión correspondiente de los alivianamientos, para que tengan una rigidez torsional apropiada. |
| A continuación se presenta la distribución cualitativa de los diagramas de momentos torsores de los nervios de la losa utilizada como ejemplo, independizando las barras orientadas en la dirección y, de las barras orientadas en la dirección x: |
| Si en lugar de utilizar el tercer modelo para losas nervadas, se empleara el tercer modelo para losas macizas, la geometría del perfil de momentos flectores alrededor del eje x sería: |
| La geometría del perfil de momentos flectores alrededor del eje y sería: |
| Si se toma el décimo modelo de losa nervada (tiene un borde libre y los otros tres bordes empotrados), con una relación lado corto / lado largo de 0.80, la estructura idealizada sería: |
| La distribución cualitativa de los momentos flectores, en las 2 direcciones principales de la losa del ejemplo, para una carga uniformemente distribuida sobre toda la superficie sería similar a la siguiente: |
| Debe observarse que los momentos flectores entre bordes sustentados a la altura del borde libre son mucho más altos que los momentos flectores correspondientes en la zona central, lo que debe reflejarse en las tablas de diseño. |
| TABLAS PARA DISEÑO DE LOSAS MACIZAS RECTANGULARES SUSTENTADAS PERIMETRALMENTE, SOMETIDAS A CARGAS DISTRIBUIDAS UNIFORMES (m = 0.20) |
| TABLAS PARA DISEÑO DE LOSAS MACIZAS RECTANGULARES SUSTENTADAS PERIMETRALMENTE, SOMETIDAS A CARGAS DISTRIBUIDAS UNIFORMES (m = 0.20) |
| TABLAS PARA DISEÑO DE LOSAS MACIZAS RECTANGULARES SUSTENTADAS PERIMETRALMENTE, SOMETIDAS A CARGAS DISTRIBUIDAS UNIFORMES (m = 0.20) |
| TABLAS PARA DISEÑO DE LOSAS MACIZAS RECTANGULARES SUSTENTADAS PERIMETRALMENTE, SOMETIDAS A CARGAS DISTRIBUIDAS UNIFORMES |
| (m = 0.20) |
| Simbología: |
| d : valor adimensional para determinar la deflexión máxima en la losa |
| D : deflexión máxima en la losa Lx : longitud más corta de la losa rectangular Ly : longitud más larga de la losa rectangular |
| E : módulo de elasticidad del concreto |
| h : espesor de la losa maciza |
| q : carga uniformemente distribuida por unidad de superficie de losa my- : valor adimensional para calcular momento flector negativo máximo alrededor del eje y myb- : valor adimensional para calcular momento flector negativo máximo de borde libre alrededor del eje y my+ : valor adimensional para calcular momento flector positivo máximo de tramo alrededor del eje y myb+ : valor adimensional para calcular momento flector positivo máximo de borde libre alrededor del eje y mx- : valor adimensional para calcular momento flector negativo máximo alrededor del eje x mxb-: valor adimensional para calcular momento flector negativo máximo de borde libre alrededor del eje x mx+ : valor adimensional para calcular momento flector positivo máximo de tramo alrededor del eje x mxb+ : valor adimensional para calcular momento flector positivo máximo de borde libre alrededor del eje x My- : momento flector negativo máximo alrededor del eje y, por metro de ancho de losa Myb- : momento flector negativo máximo de borde libre alrededor del eje y, por metro de ancho de losa My+ : momento flector positivo máximo alrededor del eje y, por metro de ancho de losa Myb+ : momento flector positivo máximo de borde libre alrededor del eje y, por metro de ancho de losa Mx- : momento flector negativo máximo alrededor del eje x, por metro de ancho de losa Mxb- : momento flector negativo máximo de borde libre alrededor del eje x, por metro de ancho de losa Mx+ : momento flector positivo máximo alrededor del eje x, por metro de ancho de losa Mxb+ : momento flector positivo máximo de borde libre alrededor del eje x, por metro de ancho de losa |
| ING. CIVIL-UNS |
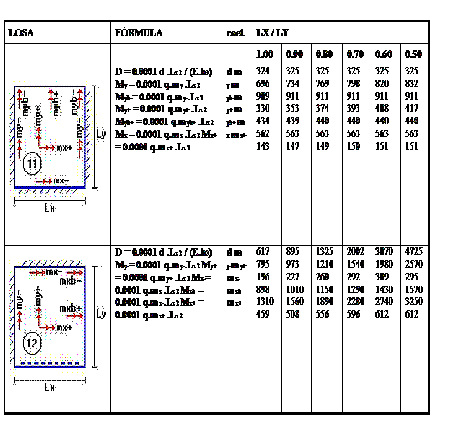
| TABLAS PARA DISEÑO DE LOSAS NERVADAS RECTANGULARES SUSTENTADAS PERIMETRALMENTE, SOMETIDAS A CARGAS DISTRIBUIDAS UNIFORMES |
| TABLAS PARA DISEÑO DE LOSAS NERVADAS RECTANGULARES SUSTENTADAS PERIMETRALMENTE, SOMETIDAS A CARGAS DISTRIBUIDAS UNIFORMES |
| Simbología: |
| d : valor adimensional para determinar la deflexión máxima en la losa D : deflexión máxima en la losa Lx : longitud más corta de la losa rectangular Ly : longitud más larga de la losa rectangular E : módulo de elasticidad del concreto h : espesor de la losa maciza q : carga uniformemente distribuida por unidad de superficie de losa my- : valor adimensional para calcular momento flector negativo máximo alrededor del eje y myb- : valor adimensional para calcular momento flector negativo máximo de borde libre alrededor del eje y my+ : valor adimensional para calcular momento flector positivo máximo de tramo alrededor del eje y myb+ : valor adimensional para calcular momento flector positivo máximo de borde libre alrededor del eje y mx- : valor adimensional para calcular momento flector negativo máximo alrededor del eje x mxb- : valor adimensional para calcular momento flector negativo máximo de borde libre alrededor del eje x mx+ : valor adimensional para calcular momento flector positivo máximo de tramo alrededor del eje x mxb+ : valor adimensional para calcular momento flector positivo máximo de borde libre alrededor del eje x My-: momento flector negativo máximo alrededor del eje y, por metro de ancho de losa Myb-: momento flector negativo máximo de borde libre alrededor del eje y, por metro de ancho de losa My+ : momento flector positivo máximo alrededor del eje y, por metro de ancho de losa Myb+ : momento flector positivo máximo de borde libre alrededor del eje y, por metro de ancho de losa Mx- : momento flector negativo máximo alrededor del eje x, por metro de ancho de losa Mxb- : momento flector negativo máximo de borde libre alrededor del eje x, por metro de ancho de losa Mx+ : momento flector positivo máximo alrededor del eje x, por metro de ancho de losa Mxb+ : momento flector positivo máximo de borde libre alrededor del eje x, por metro de ancho de losa |
| EJEMPLO 1.2: |
| Diseñar las losas del edificio, cuya planta tipo se presenta a continuación, el mismo que será utilizado para oficinas. El concreto empleado en la estructura tiene una resistencia f’c = 210 Kg/cm2, y el esfuerzo de fluencia del acero es Fy = 4200 Kg/cm2. El módulo de escaleras es independiente del bloque que se desea diseñar en este ejemplo. |
| Los pórticos 1, 2 y 3 del edificio, vistos en elevación, tienen la siguiente geometría: |
| La losa del nivel +7.50 se considera inaccesible, por lo que está sometida a una carga viva menor de 150 Kg/m2. |
| Los pórticos A, B, C y D del edificio, vistos en elevación, tienen la siguiente geometría: |
| Se selecciona un espesor tentativo de losa de 25 cm, para las tres plantas, con loseta de compresión de 5 cm., nervios de 10 cm de espesor y alivianamientos de bloque de concreto de 40 cm x 40 cm, de 20 cm de altura ( 2 bloques de 40 x 20 x 20 por cada alivianamiento), lo que es tradicional en nuestro medio. |
| Control de Deflexiones: |
| El peralte equivalente de la losa nervada se calcula determinando la altura de una losa maciza que tenga la misma inercia que la losa nervada propuesta. |
| Se calcula el área de la viga T (1 nervio de la losa): A = (5 cm x 50 cm) + (20 cm x 10 cm) = 450 cm2 Se calcula el momento que produce la viga T con respecto a su base: M = [(5 cm x 50 cm) x 22.5 cm]+ [ (20 cm x 10 cm) x 10 cm] = 7625 cm3 Se calcula la posición del centro de gravedad de la viga T con relación a la base del alma: |
| La inercia de la viga de altura constante deber ser la misma que la inercia de la viga T: |
| hequivalente = 18.06 cm |
| La ecuación básica, que define el peralte mínimo equivalente de la losa nervada es: |
| Se toma el panel 2-3-A-B, que es crítico para las deformaciones por tener las mayores luces (5 metros en las dos direcciones), y al mismo tiempo el menor número de lados con continuidad (dos de los cuatro lados son continuos): |
| Ln = 500 cm - 25 cm = 475 cm Fy = 4200 Kg/cm2 Se calculan los valores a para los cuatro bordes de la losa: |
| Eviga.Iviga = (25) (40)3 / 12 = 133333 cm4 Elosa.Ilosa = (250 - 12.5) (18.06)3 / 12 = 116583 cm4 |
| α A = α 3 = 133333 / 116583 = 1.144 |
| Eviga.Iviga = (25) (40)3 / 12 = 133333 cm4 Elosa.Ilosa = (500 - 25) (18.06)3 / 12 = 233166 cm4 a B = 133333 / 233166 = 0.572 |
| ING. CIVIL-UNS |
| Eviga.Iviga = (25) (40)3 / 12 = 133333 cm4 Elosa.Ilosa = (450 - 25) (18.06)3 / 12 = 208622 cm4 α 2 = 133333 / 208622 = 0.639 Se calcula el valor de α m : α m = (α A + α B + α 2 + α 3 ) / 4 α m = (1.144 + 0.572 + 0.639 + 1.144) / 4 = 0.875 Se calcula el coeficiente b : β = 475 / 475 = 1.00 Se calcula el coeficiente β s: β s = (5.00 + 5.00) / (5.00 + 5.00 + 5.00 + 5.00) β s = 0.50 Se calcula el valor de hmín: |
| hmín = 13.78 cm |
| Se verifica el menor valor que puede tener hmín: |
| hmín ³ 12.00 cm |
| 13.78 cm ³ 12.00 cm Þ hmín = 13.78 cm Se verifica el mayor valor que requiere tener hmín: |
| hmín £ 14.50 cm |
| 13.78 cm £ 14.50 cm Þ hmín = 13.78 cm Se verifica que la altura equivalente de la losa nervada propuesta supere la altura mínima fijada por el código: |
| hequivalente = 18.06 cm > 13.78 cm (OK) Determinación de las Cargas de Diseño en losas niveles +2.50 y +5.00: |
| Peso loseta de compresión = 1.00 x 1.00 x 0.05 x 2400 = 120 Kg/m2 Peso nervios = 4 x 0.10 x 0.20 x 1.00 x 2400 = 192 Kg/m2 Alivianamientos = 8 x 12 = 96 Kg/m2 |
| Peso Propio de la losa = 408 Kg/m2 |
| Enlucido y masillado = 1.00 x 1.00 x 0.04 x 2200 = 88 Kg/m2 Recubrimiento de piso = 1.00 x 1.00 x 0.02 x 2200 = 44 Kg/m2 Mampostería = 200 Kg/m2 |
| Carga Permanente = 740 Kg/m2 Carga Viva = 250 Kg/m2 Carga de Diseño |
| U = 1.4 D + 1.7 L = 1.4 (740) + 1.7 (250) = 1461 Kg/m2 |
| Determinación de las Cargas de Diseño en Losa Nivel +7.50 |
| D = 540 Kg/m2 (excluida la mampostería) L = 150 Kg/m2 (losa inaccesible de cubierta ) U = 1.4 D + 1.7 L = 1.4 (540) + 1.7 (150) = 1011 Kg/m2 |
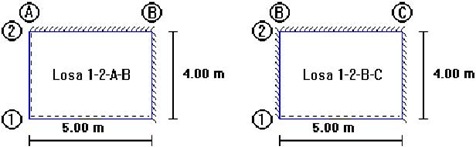
| Modelos Estructurales de Losas para el Diseño a Flexión |
| Los coeficientes para diseño de la losa 1-2-A-B se obtienen del modelo 6 de las tablas para losas nervadas, considerando que la dirección más corta está en el sentido y, lo que significa que se deben intercambiar los valores tabulados de mx y my. |
| Los coeficientes para diseño de la losa 1-2-B-C se obtienen del modelo 2 de las tablas para losas nervadas, considerando que la dirección más corta está en el sentido y, lo que significa que se deben intercambiar los valores tabulados de mx y my. |
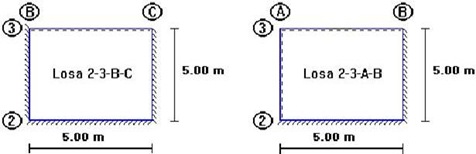
| Los coeficientes para diseño de la losa 2-3-A-B se obtienen del modelo 6 de las tablas para losas nervadas. |
| Los coeficientes para diseño de la losa 2-3-B-C se obtienen del modelo 2 de las tablas para losas nervadas, considerando un intercambio entre los ejes x, y de la tabla, por la posición de los ejes en la losa. |
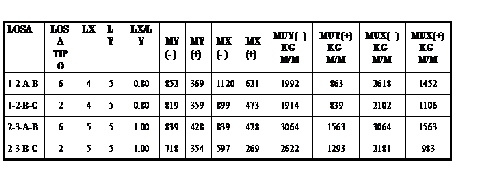
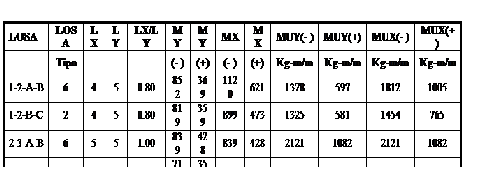
| Determinación de Momentos Flectores de Diseño y Cálculo de la Armadura Requerida |
| TABLAS PARA EL DISEÑO DE LOSAS NIVELES +2.50, +5.00 |
| q = 1461 Kg/m2 |
| M = 0.0001 m . q . Lx2 |
| TABLAS PARA EL DISEÑO DE LOSA NIVEL +7.50 |
| q = 1011 Kg/m2 M = 0.0001 m . q . Lx2 |
| Los ejes x - y de las tablas de diseño de losas sustentadas perimetralmente, no deben coincidir necesariamente con los ejes x - y del proyecto, pues de acuerdo a las convenciones empleadas, la dirección x en las tablas es la de menor dimensión de la losa. |
| La armadura mínima requerida en losas alivianadas es: |
| Asmín = 0.00333 (20 x 22) = 1.47 cm2/m |
| A continuación se presentan las tablas de armado modificadas tomando en consideración la armadura mínima requerida. |
| ARMADURA REQUERIDA EN LOSAS NIVELES +2.50, +5.00 |
| ARMADURA REQUERIDA EN LOSA NIVEL +7.50 |
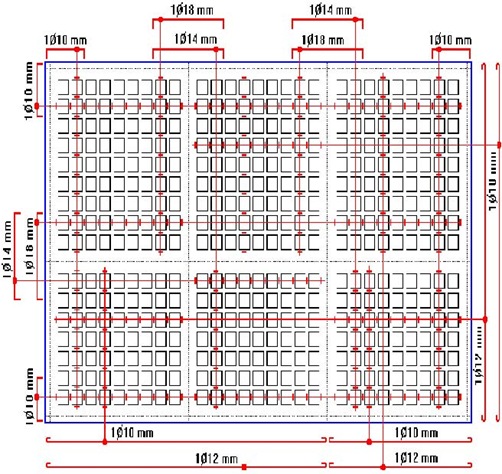
| A continuación se presenta un armado tipo de las losas del edificio, que se ajusta a las tablas anteriores. |
| ARMADURA EN LOSAS NIVELES +2.50, +5.00 |
| ARMADURA EN LOSA NIVEL +7.50 |
| Verificación de la Resistencia a Cortante: |
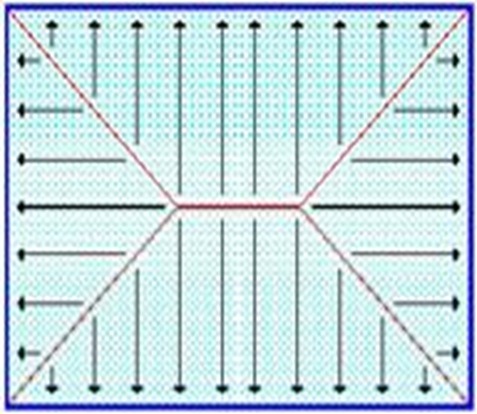
| De acuerdo con la experimentación en que se basa la Teoría de las Líneas de Rotura, cuando una losa rectangular, sustentada en todo su perímetro sobre vigas de mayor peralte y sometida a una carga uniformemente distribuida que actúa en toda su superficie, se encuentra al borde del colapso, se fisura conformando triángulos y trapecios. |
| Bajo este estado límite, las fuerzas cortantes que generan las cargas que actúan en los triángulos y trapecios se transmiten directamente a las vigas en las que se sustentan los respectivos triángulos y trapecios. |
| Las losas deben estar en capacidad de resistir las fuerzas cortantes generadas por este tipo de comportamiento. |
| Las secciones críticas de las losas, para el diseño a cortante, se ubican en los sectores de ordenada máxima de los triángulos y trapecios, proximos a las vigas de apoyo. |
| Las cargas que solicitan las secciones de cortante crítico son aquellas que actúan sobre zonas ortogonales limitadas por la línea de cortante crítico y la línea de fisuración intermedia de la losa. |
| ING. CIVIL-UNS |
| Verificación a Cortante de las Losas de 5.00 m x 5.00 m de los Niveles +2.50 y +5.00: |
| Se toma la sección de diseño con ancho unitario (un metro de ancho). La carga última superficial es: qU = 1461 Kg/m2 La sección de diseño está ubicada a 25 cm de la cara de la viga; la cara de la viga está ubicada a 12.5 cm del |
| eje de la viga, por lo que la sección de diseño se ubica a 37.5 cm del eje de la viga. |
| La fuerza cortante que actúa sobre un metro de ancho de la zona crítica a cortante es: Vu = 1.00 m x 2.125 m x 1475 Kg/m2 Vu = 3134 Kg En un metro de losa se dispone de dos nervios de 10 cm de ancho (ancho total = 20 cm), por lo que el |
| esfuerzo cortante último es: |
| vu = 8.38 Kg/ cm2 |
| El esfuerzo cortante que puede soportar el concreto es: |
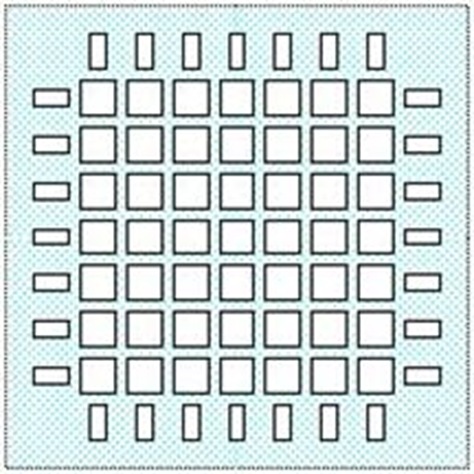
| La sección transversal no es suficiente para resistir las fuerzas cortantes. Como solución se puede incrementar el ancho de los nervios en la fila perimetral de alivianamientos, colocando un solo bloque de 20 cm x 40 cm x 20 cm en cada alivianamiento. |
| El ancho efectivo de los nervios se incrementa de 20 cm a 60 cm con lo que la capacidad resistente se triplica. El incremento de peso es mínimo, por lo que no es necesario realizar un recálculo de cargas. |
| vu = 2.79 Kg/ cm2 (O.K.) |
| Una segunda zona crítica a cortante se produce a 80 cm del eje de las vigas, donde los nervios siguen manteniendo los 10 cm de ancho (20 cm de ancho por metro). |
| La fuerza cortante que actúa sobre un metro de ancho de la segunda zona crítica a cortante es: |
| Vu = 1.00 m x 1.70 m x 1475 Kg/m2 |
| Vu = 2508 Kg El esfuerzo cortante último es: vu = 6.71 Kg/ cm2 vu < vc (O.K.) El esfuerzo cortante último es inferior a la capacidad resistente del concreto por lo que no se requiere de ningún cambio adicional en las dimensiones de los alivianamientos. |
| Verificación a Cortante de las Losas de 4.00 m x 5.00 m de los Niveles +2.50 y +5.00: |
| La fuerza cortante que actúa sobre un metro de ancho de la zona crítica a cortante es: Vu = 1.00 m x 1..625 m x 1475 Kg/m2 Vu = 2397 Kg El esfuerzo cortante último es: |
| vu = 6.41 Kg/ cm2 vu < vc (O.K.) |
| El esfuerzo cortante último es inferior a la capacidad resistente del concreto por lo que no se requiere ningún cambio en las dimensiones de los alivianamientos. |
| Verificación a Cortante de las Losas de 5.00 m x 5.00 m del Nivel +7.50: |
| qU = 1011 Kg/m2 |
| La fuerza cortante para un metro de ancho es: Vu = 1.00 m x 2.125 m x 1011 Kg/m2 Vu = 2148 Kg El esfuerzo cortante es: vu = 5.74 Kg/ cm2 vu < vc (O.K.) |
| El esfuerzo cortante último es inferior a la capacidad resistente del concreto por lo que no se requiere ningún cambio en las dimensiones de los alivianamientos. La losa de 4.00 m x 5.00 m del nivel +7.00 tampoco requiere ningún cambio. |
| Armadura de Temperatura y Retracción de Fraguado: |
| Para absorber los esfuerzos generados en el concreto de la loseta de compresión, por concepto de cambios de temperatura y retracción de fraguado, y permitir un control eficiente de la fisuración, se puede utilizar una malla electrosoldada con esfuerzo de fluencia Fy = 2800 Kg/cm2, requiriéndose la siguiente armadura mínima en las dos direcciones: |
| ρ mín = 0.0020 |
| Asmín = ρ mín . b . d |
| Asmín = (0.0020) (100 cm) (2.5 cm) |
| Asmín = 0.50 cm2 por metro de ancho |
| El máximo espaciamiento entre alambres de la malla electrosoldada es 5 veces el espesor de la loseta o 45 cm, el que sea menor: |
| emáx = 5 (5 cm) = 25 cm emáx £ 45 cm emáx = 25 cm |
| Se puede escoger una malla con alambres de 4 mm de diámetro espaciados cada 25 cm, que debe colocarse a media altura en la loseta de compresión. |
| ARMADURA Y DISTRIBUCION DE ALIVIANAMIENTOS EN LOSAS NIVELES +2.50, +5.00 |
| ARMADURA Y DISTRIBUCION DE ALIVIANAMIENTOS EN LOSA NIVEL +7.50 |
ING. CIVIL-UNS